
【題目】選修4-4:坐標系與參數方程:
已知極坐標系的極點在直角坐標系的原點,極軸與x軸非負半軸重合,直線l的參數方程為:![]() (t為參數,a∈[0,π),曲線C的極坐標方程為:p=2cosθ.
(t為參數,a∈[0,π),曲線C的極坐標方程為:p=2cosθ.
(Ⅰ)寫出曲線C在直角坐標系下的標準方程;
(Ⅱ)設直線l與曲線C相交PQ兩點,若|PQ|![]() ,求直線l的斜率.
,求直線l的斜率.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,以坐標原點O為極點,x軸正半軸為極軸建立極坐標系。已知曲線C的極坐標方程為![]() ,過點
,過點![]() 的直線l的參數方程為
的直線l的參數方程為 (為參數),直線l與曲線C交于M、N兩點。
(為參數),直線l與曲線C交于M、N兩點。
(1)寫出直線l的普通方程和曲線C的直角坐標方程:
(2)若![]() 成等比數列,求a的值。
成等比數列,求a的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一場小型晚會有![]() 個唱歌節目和
個唱歌節目和![]() 個相聲節目,要求排出一個節目單.
個相聲節目,要求排出一個節目單.
(1)![]() 個相聲節目要排在一起,有多少種排法?
個相聲節目要排在一起,有多少種排法?
(2)![]() 個相聲節目彼此要隔開,有多少種排法?
個相聲節目彼此要隔開,有多少種排法?
(3)第一個節目和最后一個節目都是唱歌節目,有多少種排法?
(4)前![]() 個節目中要有相聲節目,有多少種排法?
個節目中要有相聲節目,有多少種排法?
(要求:每小題都要有過程,且計算結果都用數字表示)
查看答案和解析>>
科目:高中數學 來源: 題型:
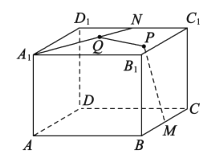
【題目】已知長方體![]() 中,底面ABCD的長AB=4,寬BC=4,高
中,底面ABCD的長AB=4,寬BC=4,高![]() =3,點M,N分別是BC,
=3,點M,N分別是BC,![]() 的中點,點P在上底面
的中點,點P在上底面![]() 中,點Q在
中,點Q在![]() 上,若
上,若![]() ,則PQ長度的最小值是
,則PQ長度的最小值是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,正四棱椎P-ABCD中,底面ABCD的邊長為2,側棱長為![]() .
.

(I)若點E為PD上的點,且PB∥平面EAC.試確定E點的位置;
(Ⅱ)在(I)的條件下,點F為線段PA上的一點且![]() ,若平面AEC和平面BDF所成的銳二面角的余弦值為
,若平面AEC和平面BDF所成的銳二面角的余弦值為![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某市高三數學復習備考情況,該市教研機構組織了一次檢測考試,并隨機抽取了部分高三理科學生數學成績繪制如圖所示的頻率分布直方圖.

(1)根據頻率分布直方圖,估計該市此次檢測理科數學的平均成績![]() ;(精確到個位)
;(精確到個位)
(2)研究發現,本次檢測的理科數學成績![]() 近似服從正態分布
近似服從正態分布![]() (
(![]() ,
,![]() 約為
約為![]() ),按以往的統計數據,理科數學成績能達到自主招生分數要求的同學約占
),按以往的統計數據,理科數學成績能達到自主招生分數要求的同學約占![]() .
.
(ⅰ)估計本次檢測成績達到自主招生分數要求的理科數學成績大約是多少分?(精確到個位)
(ⅱ)從該市高三理科學生中隨機抽取![]() 人,記理科數學成績能達到自主招生分數要求的人數為
人,記理科數學成績能達到自主招生分數要求的人數為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .(說明:
.(說明:![]() 表示
表示![]() 的概率.參考數據:
的概率.參考數據:![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】改革開放以來,人們的支付方式發生了巨大轉變.近年來,移動支付已成為主要支付方式之一.為了解某校學生上個月A,B兩種移動支付方式的使用情況,從全校所有的1000名學生中隨機抽取了100人,發現樣本中A,B兩種支付方式都不使用的有5人,樣本中僅使用A和僅使用B的學生的支付金額分布情況如下:
支付方式 | 不大于2000元 | 大于2000元 |
僅使用A | 27人 | 3人 |
僅使用B | 24人 | 1人 |
(Ⅰ)估計該校學生中上個月A,B兩種支付方式都使用的人數;
(Ⅱ)從樣本僅使用B的學生中隨機抽取1人,求該學生上個月支付金額大于2000元的概率;
(Ⅲ)已知上個月樣本學生的支付方式在本月沒有變化.現從樣本僅使用B的學生中隨機抽查1人,發現他本月的支付金額大于2000元.結合(Ⅱ)的結果,能否認為樣本僅使用B的學生中本月支付金額大于2000元的人數有變化?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com