曲線y=xlnx的切線與直線x-y+1=0平行，則切線方程為（ ）
A．x-y-3=0
B．x-y-2=0
C．x-y-1=0
D．x-y=0
【答案】
分析：利用直線平行斜率相等求出切線的斜率，再利用導數在切點處的值是曲線的切線斜率求出切線斜率，列出方程即得．
解答：解：∵切線與直線x-y+1=0平行，斜率為1，
又切線在切點x
的斜率為 y′|
x0∵y=xlnx，y'=1×lnx+x•
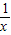
=1+lnx y'（x
）=1
1+lnx
=1，∴x
=1，
∴切點為（1，0）
切線方程為y=1×（x-1）
即x-y-1=0．
故選C．
點評：此題主要考查導數的計算，以及利用導數研究曲線上某點切線方程，屬于基礎題．
閱讀快車系列答案
