
(05年廣東卷)(14分)
在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 上異于坐標原點
上異于坐標原點![]() 的兩不同動點A、B滿足
的兩不同動點A、B滿足![]() (如圖4所示)
(如圖4所示)
(Ⅰ)求![]() 得重心
得重心![]() (即三角形三條中線的交點)
(即三角形三條中線的交點)
的軌跡方程;
(Ⅱ)![]() 的面積是否存在最小值?若存在,請求出
的面積是否存在最小值?若存在,請求出
最小值;若不存在,請說明理由.

解析: 解法一:
(Ⅰ)∵直線![]() 的斜率顯然存在,∴設直線
的斜率顯然存在,∴設直線![]() 的方程為
的方程為![]() ,
,
![]() ,依題意得
,依題意得
![]() ,①
,①
∴![]() ,②
,② ![]() ③
③
∵![]() ,∴
,∴![]() ,即
,即 ![]() ,④
,④
由③④得,![]() ,∴
,∴![]()
∴設直線![]() 的方程為
的方程為![]()
∴①可化為 ![]() ,∴
,∴![]() ⑤,
⑤,
設![]() 的重心G為
的重心G為![]() ,則
,則
![]() ⑥ ,
⑥ , ![]() ⑦,
⑦,
由⑥⑦得 ![]() ,即
,即![]() ,這就是
,這就是![]() 得重心
得重心![]() 的軌跡方程.
的軌跡方程.
(Ⅱ)由弦長公式得![]()
把②⑤代入上式,得 ![]() ,
,
設點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,則
,則![]() ,
,
∴ ![]() ,
,
∴ 當![]() ,
,![]() 有最小值,
有最小值,
∴![]() 的面積存在最小值,最小值是
的面積存在最小值,最小值是![]() .
.
解法二:
(Ⅰ)∵ AO⊥BO, 直線![]() ,
,![]() 的斜率顯然存在,
的斜率顯然存在,
∴設AO、BO的直線方程分別為![]() ,
,![]() ,
,
設![]() ,
,![]() ,依題意可得
,依題意可得
由![]() 得
得 ![]() ,由
,由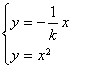 得
得 ![]() ,
,
設![]() 的重心G為
的重心G為![]() ,則
,則
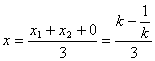 ① ,
① , 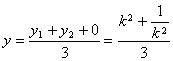 ②,
②,
由①②可得,![]() ,即為所求的軌跡方程.
,即為所求的軌跡方程.
(Ⅱ)由(Ⅰ)得,![]() ,
,![]() ,
,
∴![]()
![]()
![]() ,
,
當且僅當![]() ,即
,即![]() 時,
時,![]() 有最小值,
有最小值,
∴![]() 的面積存在最小值,最小值是
的面積存在最小值,最小值是![]() .
.
解法三:(I)設△AOB的重心為G(x , y) ,A(x1, y1),B(x2 , y2 ),則
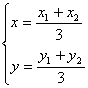 …(1)
…(1)
不過∵OA⊥OB ,
∴![]() ,即
,即![]() , …(2)
, …(2)
又點A,B在拋物線上,有![]() ,
,
代入(2)化簡得![]() ,
,
∴![]() ,
,
∴所以重心為G的軌跡方程為![]() ,
,
(II)![]() ,
,
由(I)得![]() ,
,
當且僅當![]() 即
即![]() 時,等號成立,
時,等號成立,
所以△AOB的面積存在最小值,存在時求最小值1 .


科目:高中數學 來源: 題型:
(09年江蘇百校樣本分析)(10分)挑選空軍飛行學員可以說是“萬里挑一”,要想通過需過“五關”――目測、初檢、復檢、文考、政審等. 某校甲、乙、丙三個同學都順利通過了前兩關,有望成為光榮的空軍飛行學員. 根據分析,甲、乙、丙三個同學能通過復檢關的概率分別是0.5,0.6,0.75,能通過文考關的概率分別是0.6,0.5,0.4,通過政審關的概率均為1.后三關相互獨立.
(1)求甲、乙、丙三個同學中恰有一人通過復檢的概率;
(2)設通過最后三關后,能被錄取的人數為![]() ,求隨機變量
,求隨機變量![]() 的期望
的期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
(08年莆田四中一模理) (14分)
由函數![]() 確定數列
確定數列![]() ,
,![]() ,若函數
,若函數![]() 的反函數
的反函數![]() 能確定數列
能確定數列![]() ,
,![]() ,則稱數列
,則稱數列![]() 是數列
是數列![]() 的“反數列”。
的“反數列”。
(1)若函數![]() 確定數列
確定數列![]() 的反數列為
的反數列為![]() ,求
,求![]() 的通項公式;
的通項公式;
(2)對(1)中![]() ,不等式
,不等式![]() 對任意的正整數
對任意的正整數![]() 恒成立,求實數
恒成立,求實數![]() 的范圍;
的范圍;
(3)設![]() ,若數列
,若數列![]() 的反數列為
的反數列為![]() ,
,![]() 與
與![]() 的公共項組成的數列為
的公共項組成的數列為![]() ;求數列
;求數列![]() 前
前![]() 項和
項和![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com