【答案】
分析:(Ⅰ)設出等比數列的公比q,由a
32=9a
2a
6,利用等比數列的通項公式化簡后得到關于q的方程,由已知等比數列的各項都為正數,得到滿足題意q的值,然后再根據等比數列的通項公式化簡2a
1+3a
2=1,把求出的q的值代入即可求出等比數列的首項,根據首項和求出的公比q寫出數列的通項公式即可;
(Ⅱ)把(Ⅰ)求出數列{a
n}的通項公式代入設bn=log
3a
1+log
3a
2+…+log
3a
n,利用對數的運算性質及等差數列的前n項和的公式化簡后,即可得到b
n的通項公式,求出倒數即為

的通項公式,然后根據數列的通項公式列舉出數列的各項,抵消后即可得到數列{

}的前n項和.
解答:解:(Ⅰ)設數列{a
n}的公比為q,由a
32=9a
2a
6得a
32=9a
42,所以q
2=

.
由條件可知各項均為正數,故q=

.
由2a
1+3a
2=1得2a
1+3a
1q=1,所以a
1=

.
故數列{a
n}的通項式為a
n=

.
(Ⅱ)b
n=

+

+…+

=-(1+2+…+n)=-

,
故

=-

=-2(

-

)
則

+

+…+

=-2[(1-

)+(

-

)+…+(

-

)]=-

,
所以數列{

}的前n項和為-

.
點評:此題考查學生靈活運用等比數列的通項公式化簡求值,掌握對數的運算性質及等差數列的前n項和的公式,會進行數列的求和運算,是一道中檔題.

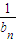 }的前n項和.
}的前n項和. 的通項公式,然后根據數列的通項公式列舉出數列的各項,抵消后即可得到數列{
的通項公式,然后根據數列的通項公式列舉出數列的各項,抵消后即可得到數列{ }的前n項和.
}的前n項和. .
. .
. .
. .
. +
+ +…+
+…+ =-(1+2+…+n)=-
=-(1+2+…+n)=- ,
, =-
=- =-2(
=-2( -
- )
) +
+ +…+
+…+ =-2[(1-
=-2[(1- )+(
)+( -
- )+…+(
)+…+( -
- )]=-
)]=- ,
, }的前n項和為-
}的前n項和為- .
.
