【題目】從裝有
個不同小球的口袋中取出
個小球（
），共有
種取法。在這種取法中，可以視作分為兩類：第一類是某指定的小球未被取到，共有
種取法；第二類是某指定的小球被取到，共有
種取法。顯然
，即有等式：
成立。試根據上述想法，下面式子
（其中
）應等于 （ ）
A. 
B. 
C. 
D. 
通城學典默寫能手系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目：高中數學 來源： 題型：
【題目】已知圓
，直線
。
（Ⅰ）求證：直線
與圓C恒有兩個交點；
（Ⅱ）求出直線
被圓C截得的最短弦長，并求出截得最短弦長時的
的值；
（Ⅲ）設直線
與圓C的兩個交點為M，N，且
（點C為圓C的圓心），求直線
的方程。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“一帶一路”是“絲綢之路經濟帶”和“21世紀海上絲綢之路”的簡稱．某市為了了解人們對“一帶一路”的認知程度，對不同年齡和不同職業的人舉辦了一次“一帶一路”知識競賽，滿分100分（90分及以上為認知程度高）.現從參賽者中抽取了
人，按年齡分成5組，第一組： 
，第二組： 
，第三組： 
，第四組： 
，第五組： 
，得到如圖所示的頻率分布直方圖，已知第一組有6人．
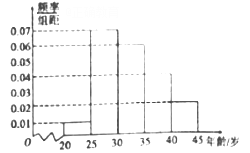
（1）求
；
（2）求抽取的人的年齡的中位數（結果保留整數）；
（3）從該市大學生、軍人、醫務人員、工人、個體戶 五種人中用分層抽樣的方法依次抽取6人，42人，36人，24人，12人，分別記為1～5組，從這5個按年齡分的組和5個按職業分的組中每組各選派1人參加知識競賽，分別代表相應組的成績，年齡組中1～5組的成績分別為93，96，97，94，90，職業組中1～5組的成績分別為93，98，94，95，90．
（Ⅰ）分別求5個年齡組和5個職業組成績的平均數和方差；
（Ⅱ）以上述數據為依據，評價5個年齡組和5個職業組對“一帶一路”的認知程度．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}的前n項和為Sn,a4=2且
,數列
滿足
,
(1)證明：數列{an}為等差數列；
(2)是否存在正整數
，
(1<
)，使得
成等比數列，若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某動物園要為剛入園的小動物建造一間兩面靠墻的三角形露天活動室，地面形狀如圖所示，已知已有兩面墻的夾角為
，墻
的長度為
米，（已有兩面墻的可利用長度足夠大），記
.
（1）若
，求
的周長（結果精確到0.01米）；
（2）為了使小動物能健康成長，要求所建的三角形露天活動室面積，的面積盡可能大，當
為何值時，該活動室面積最大？并求出最大面積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地區經過一年的新農村建設，農村的經濟收入增加了一倍，實現翻番.為更好地了解該地區農村的經濟收入變化情況，統計了該地區新農村建設前后農村的經濟收入構成比例，得到如下餅圖，則下面結論中不正確的是（ ）
建設前經濟收入構成比例 建設后經濟收入構成比例
A. 新農村建設后，養殖收入增加了一倍
B. 新農村建設后，其他收入增加了一倍以上
C. 新農村建設后，種植收入減少
D. 新農村建設后，養殖收入與第三產業收入的總和超過了經濟收入的一半
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“
”是“對任意的正數
， 
”的（ ）
A. 充分不必要條件 B. 必要不充分條件 C. 充要條件 D. 既不充分也不必要條件
【答案】A
【解析】分析：根據基本不等式，我們可以判斷出“
”?“對任意的正數x，2x+
≥1”與“對任意的正數x，2x+
≥1”?“a=
”真假，進而根據充要條件的定義，即可得到結論．
解答：解：當“a=
”時，由基本不等式可得：
“對任意的正數x，2x+
≥1”一定成立，
即“a=
”?“對任意的正數x，2x+
≥1”為真命題；
而“對任意的正數x，2x+
≥1的”時，可得“a≥
”
即“對任意的正數x，2x+
≥1”?“a=
”為假命題；
故“a=
”是“對任意的正數x，2x+
≥1的”充分不必要條件
故選A
【題型】單選題
【結束】
11
【題目】如圖，四棱錐
中， 
平面
，底面
為直角梯形， 
， 
![](http://thumb.zyjl.cn/questionBank/Upload/2018/07/26/10/1a9f63c3/SYS201807261001518656386206_ST/SYS201807261001518656386206_ST.023.png"){kind=small}
， 
，點
在棱
上，且
，則平面
與平面
的夾角的余弦值為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
．
（1）求函數
的對稱軸方程；
（2）將函數
的圖象上各點的縱坐標保持不變，橫坐標伸長為原來的2倍，然后再向左平移
個單位，得到函數
的圖象．若
， 
， 
分別是
△三個內角
， 
， 
的對邊， 
， 
，且
，求
的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
