Question

（07年天津卷理）(14分)

    在數列中N其中.

    (I)求數列的通項公式；

    (II)求數列的前項和；

    (III)證明存在N使得對任意N均成立.

Answer 1

解析：(I)解法一：，

    ，

    .

    由此可猜想出數列的通項公式為.

    以下用數學歸納法證明.

    (1)當時等式成立.

    (2)假設當時等式成立，即

那么，

這就是說，當時等式也成立.根據(1)和(2)可知，等式對任何N都成立.

解法二：由N可得

    所以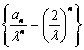為等數列，其公差為1，首項為0.故

所以數列的通項公式為

(II)設                 ①

             ②

    當時，①式減去②式，得

   

   

    這時數列的前項和

    當 時，這時數列的前項和

(III)證明：通過分析，推測數列的第一項最大.下面證明： ③

    由知要使③式成立，只要因為

   

              

    所以③式成立. 因此，存在使得對任意N均成立.

【考點】本小題以數列的遞推關系式為載體，主要考查等比數列的前項和公式、數列求和、不等式的證明等基礎知識與基本方法，考查歸納、推理、運算及靈活運用數學知識分析問題和解決問題的能力.