
【題目】某市一次全市高中男生身高統計調查數據顯示:全市10萬名男生的身高服從正態分布![]() .現從某學校高中男生中隨機抽取50名測量身高,測量發現被測學生身高全部介于160cm和190cm之間,將身高的測量結果按如下方式分成5組:第1組[160,166),第2組[166,172),...,第5組[184,190]下表是按上述分組方法得到的頻率分布表:
.現從某學校高中男生中隨機抽取50名測量身高,測量發現被測學生身高全部介于160cm和190cm之間,將身高的測量結果按如下方式分成5組:第1組[160,166),第2組[166,172),...,第5組[184,190]下表是按上述分組方法得到的頻率分布表:
分組 | [160,166) | [166,172) | [172,178) | [178,184) | [184,190] |
人數 | 3 | 10 | 24 | 10 | 3 |
這50個數據的平均數和方差分別比10萬個數據的平均數和方差多1和6.68,且這50個數據的方差為![]() .(同組中的身高數據用該組區間的中點值作代表):
.(同組中的身高數據用該組區間的中點值作代表):
(1)求![]() ,
,![]() ;
;
(2)給出正態分布的數據:![]() ,
,![]() .
.
(i)若從這10萬名學生中隨機抽取1名,求該學生身高在(169,179)的概率;
(ii)若從這10萬名學生中隨機抽取1萬名,記![]() 為這1萬名學生中身高在(169,184)的人數,求
為這1萬名學生中身高在(169,184)的人數,求![]() 的數學期望.
的數學期望.
【答案】(1) ![]() =174;
=174;![]() ; (2) (i) 0.6826 ;(ii)8185
; (2) (i) 0.6826 ;(ii)8185
【解析】
(1)由每組的中間值乘以該組的人數,再求和,最后除以總人數,即可求出平均值,根據題意即可得到![]() ,再由
,再由![]() ,以及題中條件,即可得出
,以及題中條件,即可得出![]() ;
;
(2)(i)先由題意得(169,179)=(![]() ,
,![]() ),根據題中所給數據,即可求出對應概率;
),根據題中所給數據,即可求出對應概率;
(ii)由題意可知(169,184)=(![]() ,
,![]() ),,先求出一名學生身高在(169,184)的概率,由題意可知
),,先求出一名學生身高在(169,184)的概率,由題意可知![]() 服從二項分布,再由二項分布的期望,即可求出結果.
服從二項分布,再由二項分布的期望,即可求出結果.
解:(1)根據頻率分布表中的數據可以得出這50個數據的平均數為
![]()
所以![]() ,
,
又![]() =31.68,
=31.68,
所以![]() .
.
(2) (i)由題意可知(169,179)=(![]() ,
,![]() ),
),
所以該學生身高在(169,179)的概率為p=0.6826
(ii)由題意可知(169,184)=(![]() ,
,![]() ),
),
所以一名學生身高在(169,184)的概率為![]()
根據題意![]() ,
,
所以![]() 的數學期望
的數學期望![]() .
.


 直通貴州名校周測月考直通名校系列答案
直通貴州名校周測月考直通名校系列答案 培優三好生系列答案
培優三好生系列答案科目:高中數學 來源: 題型:
【題目】一個盒子里裝有大小均勻的6個小球,其中有紅色球4個,編號分別為1,2,3,4;白色球2個,編號分別為4,5,從盒子中任取3個小球(假設取到任何—個小球的可能性相同).
(1)求取出的3個小球中,含有編號為4的小球的概率;
(2)在取出的3個小球中,小球編號的最大值設為![]() ,求隨機變量
,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖已知橢圓![]() ,
,![]() 是長軸的一個端點,弦
是長軸的一個端點,弦![]() 過橢圓的中心
過橢圓的中心![]() ,且
,且![]() ,
,![]() .
.

(Ⅰ)求橢圓的方程:
(Ⅱ)設![]() 為橢圓上異于
為橢圓上異于![]() 且不重合的兩點,且
且不重合的兩點,且![]() 的平分線總是垂直于
的平分線總是垂直于![]() 軸,是否存在實數
軸,是否存在實數![]() ,使得
,使得![]() ,若存在,請求出
,若存在,請求出![]() 的最大值,若不存在,請說明理由.
的最大值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將三棱錐![]() 與
與![]() 拼接得到如圖所示的多面體,其中
拼接得到如圖所示的多面體,其中![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() ,
,![]() 的中點,
的中點,![]() .
.
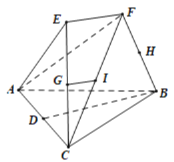
(1)當點![]() 在直線
在直線![]() 上時,證明:
上時,證明:![]() 平面
平面![]() ;
;
(2)若![]() 與
與![]() 均為面積為
均為面積為![]() 的等邊三角形,求該多面體體積的最大值.
的等邊三角形,求該多面體體積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知焦點在![]() 軸上的拋物線
軸上的拋物線![]() 過點
過點![]() ,橢圓
,橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,
,![]() ,其中
,其中![]() 與
與![]() 的焦點重合,過點
的焦點重合,過點![]() 與
與![]() 的長軸垂直的直線交
的長軸垂直的直線交![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() ,曲線
,曲線![]() 是以坐標原點
是以坐標原點![]() 為圓心,以
為圓心,以![]() 為半徑的圓.
為半徑的圓.
(1)求![]() 與
與![]() 的標準方程;
的標準方程;
(2)若動直線![]() 與
與![]() 相切,且與
相切,且與![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的面積
的面積![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com