
【題目】已知集合![]() ,
,![]() ,全集
,全集![]() .
.
(1)當![]() 時,求
時,求![]() ,
,![]() ;
;
(2)若![]() 是
是![]() 成立的充分不必要條件,求實數
成立的充分不必要條件,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)A∩B={x|1≤x≤4},(UA)∩(UB)={x|x<﹣2或x>7};(2)(﹣∞,﹣4)∪[﹣1,![]() ]
]
【解析】
(1)當![]() 時,得到
時,得到![]() ,再計算
,再計算![]() ,
,![]() 得到答案.
得到答案.
(2)將充分不必要條件轉化為AB,再討論![]() 和
和![]() 兩種情況,分別計算得到答案.
兩種情況,分別計算得到答案.
(1)當a=2時,A={x|1≤x≤7},則A∩B={x|1≤x≤4};
UA={x|x<1或x>7},UB={x|x<﹣2或x>4},
(UA)∩(RB)={x|x<﹣2或x>7};
(2)∵x∈A是x∈B成立的充分不必要條件,∴AB,
①若A=,則a﹣1>2a+3,解得a<﹣4;
②若A≠,由AB,得到,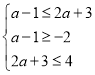 且a﹣1≥﹣2與2a+3≤4不同時取等號
且a﹣1≥﹣2與2a+3≤4不同時取等號
解得:﹣1≤a![]() ,
,
綜上所述:a的取值范圍是(﹣∞,﹣4)∪[﹣1,![]() ].
].


科目:高中數學 來源: 題型:
【題目】下列命題正確的是( )
A. 命題“若![]() ,則
,則![]() ”的逆否命題為真命題;
”的逆否命題為真命題;
B. 命題“![]() ”為假命題,則命題
”為假命題,則命題![]() 與命題
與命題![]() 都是假命題;
都是假命題;
C. “![]() ”是“
”是“![]() ”成立的必要不充分條件;
”成立的必要不充分條件;
D. 命題“存在![]() ,使得
,使得![]() ”的否定是:“對任意
”的否定是:“對任意![]() ,均有
,均有![]() ”.
”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,焦距為
,焦距為![]() ,直線
,直線![]() 過橢圓的
過橢圓的![]() 左焦點.
左焦點.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() 與
與![]() 軸交于點
軸交于點![]() 是橢圓
是橢圓![]() 上的兩個動點,
上的兩個動點,![]() 的平分線在
的平分線在![]() 軸上,
軸上,![]() .試判斷直線
.試判斷直線![]() 是否過定點,若過定點,求出定點坐標;若不過定點,請說明理由.
是否過定點,若過定點,求出定點坐標;若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 過定點
過定點![]() ,并且內切于定圓
,并且內切于定圓![]() ..
..
(1)求動圓圓心![]() 的軌跡方程;
的軌跡方程;
(2)若![]() 上存在兩個點
上存在兩個點![]() ,(1)中曲線上有兩個點
,(1)中曲線上有兩個點![]() ,并且
,并且![]() 三點共線,
三點共線,![]() 三點共線,
三點共線,![]() ,求四邊形
,求四邊形![]() 的面積的最小值.
的面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年1月1日起我國實施了個人所得稅的新政策,其政策的主要內容包括:(1)個稅起征點為5000元;(2)每月應納稅所得額(含稅)=收入-個稅起征點-專項附加扣除;(3)專項附加扣除包括:①贍養老人費用,②子女教育費用,③繼續教育費用,④大病醫療費用等,其中前兩項的扣除標準為:①贍養老人費用:每月扣除2000元,②子女教育費用:每個子女每月扣除1000元,新的個稅政策的稅率表部分內容如下:
級數 | 一級 | 二級 | 三級 |
每月應納稅所得額 |
|
|
|
稅率 | 3 | 10 | 20 |
現有李某月收入為18000元,膝下有一名子女在讀高三,需贍養老人,除此之外無其它專項附加扣除,則他該月應交納的個稅金額為( )
A.1800B.1000C.790D.560
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com