過曲線C:f(x)=x3-ax+b外的點A(1,0)作曲線C的切線恰有兩條,
(1)求a,b滿足的等量關系;
(2)若存在x0∈R+,使f(x0)>x0•ex0+a成立,求a的取值范圍.
分析:(1)設出切點,求出切點處的導函數即切線的斜率,據點斜式寫出切線的方程,將切點代入,列出關于切點橫坐標的方程,據題意此方程有兩個根,構造函數,通過導函數求出兩個極值,令極值為0,求出a,b的關系.
(2)寫出不等式,分離出參數a,構造函數g(x),將問題轉化為a<g(x)的最大值;通過對g(x)求兩階導數求g(x)的最值.
解答:解:(1)f′(x)=3x2-a,
過點A(1,0)作曲線C的切線,設切點(x0,f(x0)),則切線方程為:y=(3x02-a)(x-1)
將(x0,f(x0))代入得:f(x0)=(3x02-a)(x0-1)=x03-ax0+b
即2x03-3x02+a-b=0(*) 由條件切線恰有兩條,方程(*)恰有兩根.
令u(x)=2x3-3x2+a-b,u′(x)=6x2-6x=6x(x-1),顯然有兩個極值點x=0與x=1,
于是u(0)=0或u(1)=0
當u(0)=0時,a=b;
當u(1)=0時,a-b=1,此時f(x)=x3-ax+a-1=(x-1)(x2+x+1-a)經過(1,0)與條件不符
所以a=b
(2)因為存在x0∈R+,使f(x0)>x0•ex0+a,即x03-ax0+a>x0•ex0+a
所以存在x0∈R+,使x03-ax0>x0•ex0,得x02-a>ex0,即a<x02-ex0成立
設g(x)=x2-ex(x>0),問題轉化為a<g(x)的最大值
g′(x)=2x-ex,
g′′(x)=2-ex,令g′′(x)=0得x=ln2,
當x∈(0,ln2)時g′′(x)>0此時g′(x)為增函數,當x∈(ln2,+∞)時g′′(x)<0,此時g′(x)為減函數,
所以g′(x)的最大值為g′(ln2)=2ln2-eln2=2ln2-2=2(ln2-1)
∵ln2<1,∴g′(x)的最大值g′(ln2)<0,得g′(x)<0
所以g(x)在(0,+∞)上單調遞減,g(x)<g(0)=-1
因此a≤-1.
點評:求曲線的切線問題常利用導數的幾何意義:在切點處的導數值為曲線的切線斜率;解決不等式恒成立問題常采用分離參數轉化為求函數的最值.



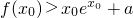 成立,求a的取值范圍.
成立,求a的取值范圍.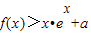 成立,求a的取值范圍.
成立,求a的取值范圍.