
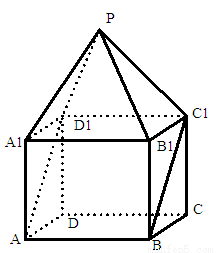
如圖,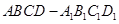 是棱長為1的正方體,四棱錐
是棱長為1的正方體,四棱錐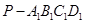 中,
中, 平面
平面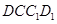 ,
,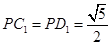 。
。
(Ⅰ)求證: 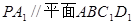
(Ⅱ)求直線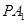 與平面
與平面 所成角的正切值。
所成角的正切值。
(Ⅰ) 先證明四邊形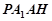 為平行四邊形,∴
為平行四邊形,∴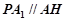 ,再利用線面平行的性質定理證明即可; (Ⅱ)
,再利用線面平行的性質定理證明即可; (Ⅱ)

【解析】
試題分析:(Ⅰ)取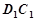 的中點
的中點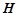 ,連結
,連結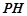 ,
,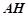 .
.

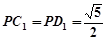 ,
,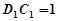 ,
,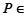 平面
平面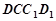 ,
,
∴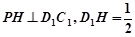 ,
,
∴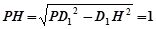 , ……1分
, ……1分
∴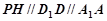 ,
, 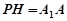 ,
,
∴四邊形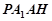 為平行四邊形,
為平行四邊形,
∴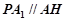 , ……3分
, ……3分
又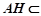 平面
平面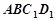 ,
,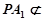 平面
平面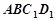 ,∴
,∴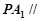 平面
平面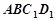 . ……5分
. ……5分
(Ⅱ)∵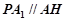 ,
,
∴直線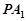 與平面
與平面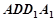 所成角等于直線
所成角等于直線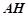 與平面
與平面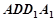 所成角.
所成角.
正方體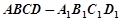 中,顯然
中,顯然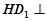 平面
平面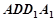 ,
,
∴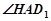 就是直線
就是直線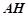 與平面
與平面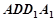 所成角. ……7分
所成角. ……7分
在 中,
中,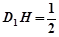 ,
, ,
,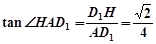 ,
,
∴直線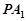 與平面
與平面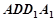 所成角的正切值為
所成角的正切值為 . ……10分
. ……10分
考點:本小題主要考查線面平行的證明,線面角的求解.
點評:要解決立體幾何問題,要發揮空間想象能力,緊扣相應的判定定理和性質定理,定理中要求的條件要一一列舉出來,求相應角時,要注意角的范圍.


科目:高中數學 來源: 題型:
 如圖,棱長為1的正四面體ABCD中,E、F分別是棱AD、CD的中點,O是點A在平面BCD內的射影.
如圖,棱長為1的正四面體ABCD中,E、F分別是棱AD、CD的中點,O是點A在平面BCD內的射影.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
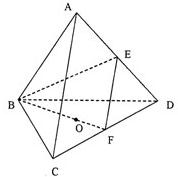 如圖,棱長為1的正四面體ABCD中,E、F分別是棱AD、CD的中點,O是點A在平面BCD內的射影.
如圖,棱長為1的正四面體ABCD中,E、F分別是棱AD、CD的中點,O是點A在平面BCD內的射影.查看答案和解析>>
科目:高中數學 來源: 題型:
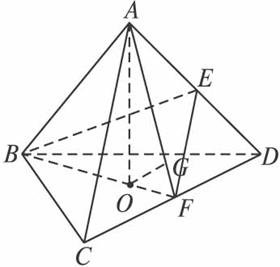
(1)求直線EF與直線BC所成角的大小;
(2)求點O到平面ACD的距離;
(3)(理)求二面角ABEF的大小.
(文)求二面角CBFE的大小.
查看答案和解析>>
科目:高中數學 來源:2007年北京市朝陽區高考數學一模試卷(理科)(解析版) 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2009-2010學年度新課標高二下學期數學單元測試1-理科 題型:解答題
如圖,把邊長為a的正六邊形紙板剪去相同的六個角,做成一個底面為正六邊形的無蓋六棱柱盒子,設高為h所做成的盒子體積V(不計接縫).
(1)寫出體積V與高h的函數關系式;
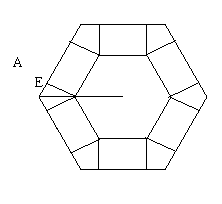 (2)當
(2)當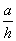 為多少時,體積V最大,最大值是多少?
為多少時,體積V最大,最大值是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com