
【題目】某地隨著經濟的發展,居民收入逐年增長,下表是該地一建設銀行連續五年的儲蓄存款(年底余額),如下表1:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
儲蓄存款 | 5 | 6 | 7 | 8 | 10 |
為了研究計算的方便,工作人員將上表的數據進行了處理,![]() ,
,![]() 得到下表2:
得到下表2:
時間代號 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(Ⅱ)通過(Ⅰ)中的方程,求出![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(Ⅲ)用所求回歸方程預測到2020年年底,該地儲蓄存款額可達多少?
(附:對于線性回歸方程![]()
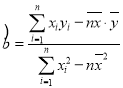
![]() )
)
 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源: 題型:
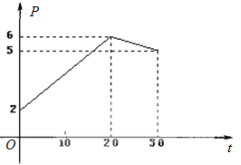
【題目】某上市股票在30天內每股的交易價格![]() (元)與時間
(元)與時間![]() (天)組成有序數對
(天)組成有序數對![]() ,點
,點![]() 落在圖中的兩條線段上.
落在圖中的兩條線段上.
該股票在30天內的日交易量![]() (萬股)與時間
(萬股)與時間![]() (天)的部分數據如下表所示:
(天)的部分數據如下表所示:
第 | 4 | 10 | 16 | 22 |
| 36 | 30 | 24 | 18 |
(1)根據提供的圖象,寫出該股票每股交易價格![]() (元)與時間
(元)與時間![]() (天)所滿足的函數關系式;
(天)所滿足的函數關系式;
(2)根據表中數據,寫出日交易量![]() (萬股)與時間
(萬股)與時間![]() (天)的一次函數關系式;
(天)的一次函數關系式;
(3)用![]() (萬元)表示該股票日交易額,寫出
(萬元)表示該股票日交易額,寫出![]() 關于
關于![]() 的函數關系式,并求在這30天內第幾天日交易額最大,最大值為多少?
的函數關系式,并求在這30天內第幾天日交易額最大,最大值為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn,n∈N*.已知a1=1,a2=![]() ,a3=
,a3=![]() ,且當n≥2時,4Sn+2+5Sn=8Sn+1+Sn-1.
,且當n≥2時,4Sn+2+5Sn=8Sn+1+Sn-1.
(1)求a4的值;
(2)證明:![]() 為等比數列;
為等比數列;
(3)求數列{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{an}是等差數列,{bn}是等比數列,且b2=3,b3=9,a1=b1,a14=b4.
(1)求{an}的通項公式;
(2)設cn=an+bn,求數列{cn}的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過定點P(-2,1)作直線l分別與x、y軸交于A、B兩點,
(1)求經過點P且在兩坐標軸上的截距相等的直線l方程.
(2)求使![]() 面積為4時的直線l方程。
面積為4時的直線l方程。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法:
①分類變量![]() 與
與![]() 的隨機變量
的隨機變量![]() 越大,說明“
越大,說明“![]() 與
與![]() 有關系”的可信度越大.
有關系”的可信度越大.
②以模型![]() 去擬合一組數據時,為了求出回歸方程,設
去擬合一組數據時,為了求出回歸方程,設![]() ,將其變換后得到線性方程
,將其變換后得到線性方程![]() ,則
,則![]() 的值分別是
的值分別是![]() 和0.3.
和0.3.
③根據具有線性相關關系的兩個變量的統計數據所得的回歸直線方程為![]() 中,
中, ![]() ,
,
則![]() .正確的個數是( )
.正確的個數是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 的圖像經過坐標原點,其到函數為
的圖像經過坐標原點,其到函數為![]() ,數列的前
,數列的前![]() 項和為
項和為![]() ,點
,點![]()
![]() 均在函數
均在函數![]() 的圖像上.
的圖像上.
(I)求數列![]() 的通項公式;
的通項公式;
(Ⅱ)設![]() ,
,![]() 是數列
是數列![]() 的前
的前![]() n項和,求使得
n項和,求使得![]() <
<![]() 對所有都成立的最小正整數m.
對所有都成立的最小正整數m.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l:4x+3y+10=0,半徑為2的圓C與l相切,圓心C在x軸上且在直線l的右上方.
(1)求圓C的方程;
(2)過點M(1,0)的直線與圓C交于A,B兩點(A在x軸上方),問在x軸正半軸上是否存在定點N,使得x軸平分∠ANB?若存在,請求出點N的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com