
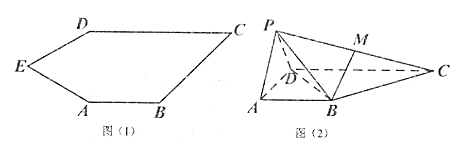
【題目】如圖(1)五邊形![]() 中,
中, ![]()
![]() ,將
,將![]() 沿
沿![]() 折到
折到![]() 的位置,得到四棱錐
的位置,得到四棱錐![]() ,如圖(2),點
,如圖(2),點![]() 為線段
為線段![]() 的中點,且
的中點,且![]() 平面
平面![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若四棱柱![]() 的體積為
的體積為![]() ,求四面體
,求四面體![]() 的體積.
的體積.
【答案】(1)詳見解析;(2)![]() .
.
【解析】試題分析:
(1)要證兩平面垂直,就要證線面垂直,首先利用已知條件![]() 與平面
與平面![]() 垂直,為此取
垂直,為此取![]() 的中點
的中點![]() ,可證得四邊形
,可證得四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() ,從而
,從而![]() 平面
平面![]() ,也即
,也即
![]() .于是由
.于是由![]() 即
即![]() 及
及![]() 為
為![]() 的中點,可得
的中點,可得![]() 為等邊三角形,
為等邊三角形,
![]() ,由
,由![]() ,得
,得![]() ,
, ![]() ,可得
,可得![]() 平面
平面![]() 平面
平面![]() 平面
平面![]() .
.
(2)利用棱錐體積公式![]() ,三棱錐
,三棱錐![]() 的底面
的底面![]() 的面積是四棱錐
的面積是四棱錐![]() 的底面
的底面![]() 面積的
面積的![]() ,高為其一半,由體積公式可得結論.
,高為其一半,由體積公式可得結論.
試題解析:
(1)證明:取![]() 的中點
的中點![]() ,連接
,連接![]() ,則
,則![]() ,
,
又![]() ,所以
,所以![]() ,則四邊形
,則四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
由![]() 即
即![]() 及
及![]() 為
為![]() 的中點,可得
的中點,可得![]() 為等邊三角形,
為等邊三角形,
∴![]() ,
,
又![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 平面
平面![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)解:設四棱錐![]() 的高為
的高為![]() ,四邊形
,四邊形![]() 的面積為
的面積為![]() ,
,
則![]() ,
,
又![]() ,四面體
,四面體![]() 底面
底面![]() 上的高為
上的高為![]() .
.
∴![]() ,
,
所以四面體![]() 的體積為
的體積為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 的底面是正方形,每條側棱的長都是底面邊長的
的底面是正方形,每條側棱的長都是底面邊長的![]() 倍,
倍,![]() 為側棱
為側棱![]() 上的點.
上的點.
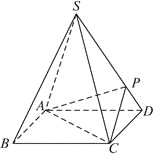
(1)求證:![]() .
.
(2)若![]() ⊥平面
⊥平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
(3)在(2)的條件下,側棱SC上是否存在一點E,使得BE∥平面PAC?若存在,求SE∶EC的值;若不存在,試說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(n)=1+ ![]() +
+ ![]() +…+
+…+ ![]() .經計算得f(4)>2,f(8)>
.經計算得f(4)>2,f(8)> ![]() ,f(16)>3,f(32)>
,f(16)>3,f(32)> ![]() .
.
(1)由上面數據,試猜想出一個一般性結論;
(2)用數學歸納法證明你的猜想.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在三棱柱ABC﹣A1B1C1中,AA1⊥底面A1B1C1 , 底面為直角三角形,∠ACB=90°,AC=2,BC=1,CC1= ![]() ,P是BC1上一動點,則A1P+PC的最小值是 .
,P是BC1上一動點,則A1P+PC的最小值是 . 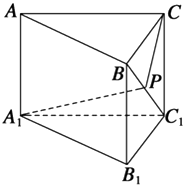
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD,PB⊥AC,Q是線段PB的中點. (Ⅰ)求證:AB⊥平面PAC;
(Ⅱ)求證:AQ∥平面PCD.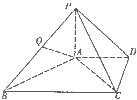
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知圓C:x2+y2=4和直線l:x=4,M為l上一動點,A1 , A2為圓C與x軸的兩個交點,直線MA1 , MA2與圓C的另一個交點分別為P、Q.
(1)若M點的坐標為(4,2),求直線PQ方程;
(2)求證直線PQ過定點,并求出此定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某地區觀眾對大型綜藝活動《中國好聲音》的收視情況,隨機抽取了100名
觀眾進行調查,其中女性有55名.下面是根據調查結果繪制的觀眾收看該節目的場數與所對應的人數表:
場數 | 9 | 10 | 11 | 12 | 13 | 14 |
人數 | 10 | 18 | 22 | 25 | 20 | 5 |
將收看該節目場次不低于13場的觀眾稱為“歌迷”,已知“歌迷”中有10名女性.
(Ⅰ)根據已知條件完成下面的2×2列聯表,并據此資料我們能否有95%的把握認為“歌迷”與性別有關?
非歌迷 | 歌迷 | 合計 | |
男 | |||
女 | |||
合計 |
(Ⅱ)將收看該節目所有場次(14場)的觀眾稱為“超級歌迷”,已知“超級歌迷”中有2名女性,若從“超級歌迷”中任意選取2人,求至少有1名女性觀眾的概率.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
參考公式與數據: 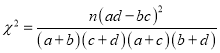 ,其中
,其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設命題p:若實數x滿足x2﹣4ax+3a2≤0,其中a>0;命題q:實數x滿足 ![]()
(1)若a=1且p∧q為真,求實數x的取值范圍;
(2)若¬p是¬q的充分不必要條件,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com