
【題目】如圖,四棱錐 ![]() 底面為正方形,已知
底面為正方形,已知 ![]() ,
,![]() ,點
,點 ![]() 為線段
為線段 ![]() 上任意一點(不含端點),點
上任意一點(不含端點),點 ![]() 在線段
在線段 ![]() 上,且
上,且 ![]() .
.
(1)求證:![]() ;
;
(2)若 ![]() 為線段
為線段 ![]() 中點,求直線
中點,求直線 ![]() 與平面
與平面 ![]() 所成的角的余弦值.
所成的角的余弦值.
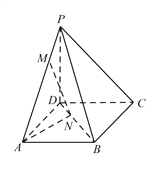
【答案】(1)見解析(2)![]()
【解析】試題分析:(1)延長![]() ,交
,交![]() 于點
于點![]() ,由相似三角形的性質可知
,由相似三角形的性質可知 ![]() ,從而得
,從而得![]() ,利用線面平行的判定定理可得直線
,利用線面平行的判定定理可得直線![]() 平面
平面![]() ;(2)由于
;(2)由于 ![]() ,
,![]() ,
,![]() 兩兩垂直,所以,以
兩兩垂直,所以,以![]() 為
為![]() 軸建立空間直角坐標系,設
軸建立空間直角坐標系,設 ![]() ,求出相關點的坐標及直線
,求出相關點的坐標及直線 ![]() 的方向向量,根據向量垂直數量積為零列方程組,求出平面
的方向向量,根據向量垂直數量積為零列方程組,求出平面 ![]() 的一個法向量,空間向量夾角余弦公式,可求解
的一個法向量,空間向量夾角余弦公式,可求解![]() 與平面
與平面 ![]() 夾角的正弦值,進而可求余弦值.
夾角的正弦值,進而可求余弦值.
試題解析:(1) 延長 ![]() ,交
,交 ![]() 于點
于點 ![]() ,連接
,連接 ![]() ,
,
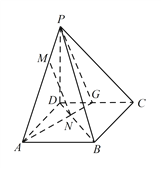
由相似知 ![]() ,可得:
,可得:![]() ,
,
![]() ,
,![]() ,
,
則 ![]() .
.
(2) 由于 ![]() ,
,![]() ,
,![]() 兩兩垂直,
兩兩垂直,
以 ![]() ,
,![]() ,
,![]() 為
為 ![]() ,
,![]() ,
,![]() 軸建立空間直角坐標系,
軸建立空間直角坐標系,
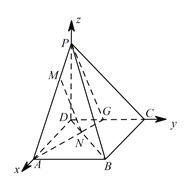
設 ![]() ,則
,則 ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
則 ![]() ,平面
,平面 ![]() 的法向量為
的法向量為 ![]() ,
,
設向量 ![]() 與
與 ![]() 的夾角為
的夾角為 ![]() ,則
,則 ![]() ,
,
則 ![]() 與平面
與平面 ![]() 夾角的余弦值為
夾角的余弦值為 ![]() .
.
【方法點晴】本題主要考查線面平行的判定定理以及利用空間向量求線面角,屬于難題.空間向量解答立體幾何問題的一般步驟是:(1)觀察圖形,建立恰當的空間直角坐標系;(2)寫出相應點的坐標,求出相應直線的方向向量;(3)設出相應平面的法向量,利用兩直線垂直數量積為零列出方程組求出法向量;(4)將空間位置關系轉化為向量關系;(5)根據定理結論求出相應的角和距離.


 課課練江蘇系列答案
課課練江蘇系列答案 名牌中學課時作業系列答案
名牌中學課時作業系列答案 明天教育課時特訓系列答案
明天教育課時特訓系列答案 浙江新課程三維目標測評課時特訓系列答案
浙江新課程三維目標測評課時特訓系列答案科目:高中數學 來源: 題型:
【題目】已知⊙H被直線x-y-1=0,x+y-3=0分成面積相等的四個部分,且截x軸所得線段的長為2。
(I)求⊙H的方程;
(Ⅱ)若存在過點P(0,b)的直線與⊙H相交于M,N兩點,且點M恰好是線段PN的中點,求實數b的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,圓
,圓![]() ,點
,點![]() 是圓上一動點,
是圓上一動點, ![]() 的垂直平分線與
的垂直平分線與![]() 交于點
交于點![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,過點
,過點![]() 且斜率不為0的直線
且斜率不為0的直線![]() 與
與![]() 交于
交于![]() 兩點,點
兩點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,證明直線
,證明直線![]() 過定點,并求
過定點,并求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某P2P平臺需要了解該平臺投資者的大致年齡分布,發現其投資者年齡大多集中在區間[20,50]歲之間,對區間[20,50]歲的人群隨機抽取20人進行了一次理財習慣調查,得到如下統計表和各年齡段人數頻率分布直方圖:
組數 | 分組 | 人數(單位:人) |
第一組 | [20,25) | 2 |
第二組 | [25,30) | a |
第三組 | [30,35) | 5 |
第四組 | [35,40) | 4 |
第五組 | [40,45) | 3 |
第六組 | [45,50] | 2 |

(Ⅰ)求a的值并畫出頻率分布直方圖;
(Ⅱ)在統計表的第五與第六組的5人中,隨機選取2人,求這2人的年齡都小于45歲的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車給市民出行帶來了諸多便利,某公司購買了一批單車投放到某地給市民使用.據市場分析,每輛單車的營運累計收入![]() (單位:元)與營運天數
(單位:元)與營運天數![]() 滿足
滿足![]() .
.
(1)要使營運累計收入高于800元,求營運天數的取值范圍;
(2)每輛單車營運多少天時,才能使每天的平均營運收入最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題![]() :若關于
:若關于![]() 的方程
的方程![]() 無實數根,則
無實數根,則![]() ;命題
;命題![]() :若關于
:若關于![]() 的方程
的方程![]() 有兩個不相等的正實數根,則
有兩個不相等的正實數根,則![]() .
.
(1)寫出命題![]() 的否命題,并判斷命題
的否命題,并判斷命題![]() 的真假;
的真假;
(2)判斷命題“![]() 且
且![]() ”的真假,并說明理由.
”的真假,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司經營一種二手機械,對該型號機械的使用年數![]() 與再銷售價格
與再銷售價格![]() (單位:百萬元/臺)進行統計整理,得到如下關系:
(單位:百萬元/臺)進行統計整理,得到如下關系:
使用年數 | 2 | 4 | 6 | 8 | 10 |
再銷售價格 | 16 | 13 | 9.5 | 7 | 5 |
(1)求![]() 關于
關于![]() 的回歸直線方程
的回歸直線方程![]() ;
;
(2)該機械每臺的收購價格為![]() (百萬元),根據(1)中所求的回歸方程,預測
(百萬元),根據(1)中所求的回歸方程,預測![]() 為何值時,此公司銷售一臺該型號二手機械所獲得的利潤
為何值時,此公司銷售一臺該型號二手機械所獲得的利潤![]() 最大?
最大?
附:參考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)對任意的m,n∈R都有f(m+n)=f(m)+f(n)-1,并且x>0時,恒有f(x)>1.
(1)求證:f(x)在R上是增函數;
(2)若f(3)=4,解不等式f(a2+a-5)<2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com