
 ,CD=2
,CD=2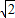 ,DE=
,DE=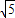 ,取CD的中點G,則EG⊥CD,利用等面積可得CF,從而可求二面角C-DE-A的正切值.
,取CD的中點G,則EG⊥CD,利用等面積可得CF,從而可求二面角C-DE-A的正切值.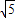 ,CD=2
,CD=2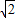 ,DE=
,DE= ,
,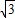 ,
,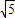 ×CF=2
×CF=2 ×
× ,
, ,
,
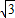 ,∴OF=
,∴OF=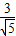 ,
,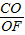 =
= =
= .
.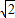 ,EG=
,EG= ,BE=
,BE= ,BG⊥CD,
,BG⊥CD, .
.

 53天天練系列答案
53天天練系列答案科目:高中數學 來源: 題型:
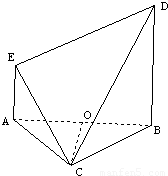
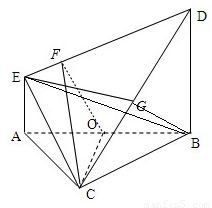
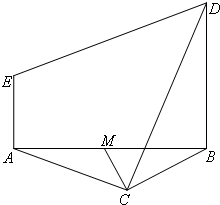 如圖,等邊△ABC與直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M為AB的中點.
如圖,等邊△ABC與直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M為AB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:
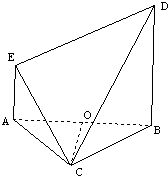 如圖,等邊△ABC與直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O為AB的中點.
如圖,等邊△ABC與直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O為AB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,等邊△ABC與直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O為AB的中點.
如圖,等邊△ABC與直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O為AB的中點.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:
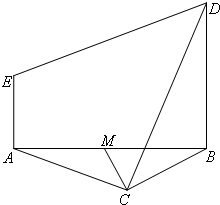
(Ⅰ)證明:CO⊥DE;
(Ⅱ)求二面角C—DE—A的大小.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com