
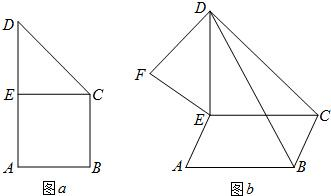
 如圖a,直角梯形ABCD中,∠A=∠B=90°,AB=BC=
如圖a,直角梯形ABCD中,∠A=∠B=90°,AB=BC= AD=1,E是底邊AD的中點,沿CE將△CDE折起,使A-CE-D是直二面角(如圖b).在圖b中過D作DF⊥平面BCD,EF∥平面BCD.
AD=1,E是底邊AD的中點,沿CE將△CDE折起,使A-CE-D是直二面角(如圖b).在圖b中過D作DF⊥平面BCD,EF∥平面BCD. ,直接計算知
,直接計算知 ,
, ,AE=1,
,AE=1, ,
, ,
,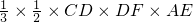
 ,
, .
. ,
, ,
, ,
, ,
, ,即
,即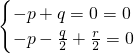 ,
,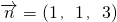 ,面ACE的一個法向量為
,面ACE的一個法向量為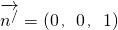 ,
, .
. ,根據數量積的幾何意義,
,根據數量積的幾何意義, .
. 

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
 如圖a,直角梯形ABCD中,∠A=∠B=90°,AB=BC=
如圖a,直角梯形ABCD中,∠A=∠B=90°,AB=BC=| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=
如圖,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=| 2 |
查看答案和解析>>
科目:高中數學 來源:2010年廣東省江門市高考數學后階段備考指導和猜題試卷(解析版) 題型:解答題
 AD=1,E是底邊AD的中點,沿CE將△CDE折起,使A-CE-D是直二面角(如圖b).在圖b中過D作DF⊥平面BCD,EF∥平面BCD.
AD=1,E是底邊AD的中點,沿CE將△CDE折起,使A-CE-D是直二面角(如圖b).在圖b中過D作DF⊥平面BCD,EF∥平面BCD.
查看答案和解析>>
科目:高中數學 來源:2011年高考數學綜合復習試卷(2)(解析版) 題型:解答題
 AD=1,E是底邊AD的中點,沿CE將△CDE折起,使A-CE-D是直二面角(如圖b).在圖b中過D作DF⊥平面BCD,EF∥平面BCD.
AD=1,E是底邊AD的中點,沿CE將△CDE折起,使A-CE-D是直二面角(如圖b).在圖b中過D作DF⊥平面BCD,EF∥平面BCD.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com