
【題目】已知拋物線![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,分別過
兩點,分別過![]() ,
,![]() 作拋物線
作拋物線![]() 的切線,兩切線交于點
的切線,兩切線交于點![]() .
.
(1)若直線![]() 變動時,點
變動時,點![]() 始終在以
始終在以![]() 為直徑的圓上,求動點
為直徑的圓上,求動點![]() 的軌跡方程;
的軌跡方程;
(2)設(shè)圓![]() ,若直線
,若直線![]() 與圓
與圓![]() 相切于點
相切于點![]() (點
(點![]() 在線段
在線段![]() 上).是否存在點
上).是否存在點![]() 使得
使得![]() ?若存在,求出點
?若存在,求出點![]() 坐標(biāo),若不存在,說明理由.
坐標(biāo),若不存在,說明理由.
【答案】(1)![]() (2)存在;點
(2)存在;點![]()
【解析】
(1)利用導(dǎo)數(shù)可求得切線![]() 的方程,進(jìn)而得到
的方程,進(jìn)而得到![]() ,由
,由![]() 可求得
可求得![]() ,進(jìn)而得到軌跡方程;
,進(jìn)而得到軌跡方程;
(2)設(shè)直線![]() 方程為
方程為![]() ,與拋物線方程聯(lián)立,利用
,與拋物線方程聯(lián)立,利用![]() 可求得
可求得![]() ;根據(jù)直線
;根據(jù)直線![]() 與圓
與圓![]() 相切可求得
相切可求得![]() ,進(jìn)而得到
,進(jìn)而得到![]() 方程,確定
方程,確定![]() 點坐標(biāo).
點坐標(biāo).
(1)設(shè)點![]() ,
,![]() ,
,![]() ,
,
由![]() 得:
得:![]() ,
,![]() ,
,
切線![]() 方程為:
方程為:![]() ,即
,即![]() ;
;
切線![]() 方程為:
方程為:![]() ,即
,即![]() ;
;
![]() ,
,![]() ,兩式消去
,兩式消去![]() 得:
得:![]() ,
,
![]() 始終在以
始終在以![]() 為直徑的圓上,
為直徑的圓上,![]() ,
,![]() ,
,![]() ,
,
![]() 點
點![]() 的軌跡方程為
的軌跡方程為![]() .
.
(2)由題意可知:直線![]() 斜率存在,設(shè)直線
斜率存在,設(shè)直線![]() 方程為:
方程為:![]() ,
,
![]() 直線
直線![]() 與圓相切,
與圓相切,![]() ,即
,即![]() ,
,
設(shè)點![]() ,
,![]() ,
,
由![]() 得:
得:![]() ,則
,則![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,解得:
,解得:![]() ,
,
![]() ,
,![]() 直線
直線![]() 方程為:
方程為:![]() ,
,![]() ,
,
即存在點![]() ,使得
,使得![]() .
.


 一諾書業(yè)暑假作業(yè)快樂假期云南美術(shù)出版社系列答案
一諾書業(yè)暑假作業(yè)快樂假期云南美術(shù)出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=2|x+1|+|x-2|.
(1)求f(x)的最小值m;
(2)若a,b,c均為正實數(shù),且滿足a+b+c=m,求證:![]() +
+![]() +
+![]() ≥3.
≥3.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的前
的前![]() 項和
項和![]() 滿足
滿足![]() ,數(shù)列
,數(shù)列![]() 滿足
滿足![]() .
.
![]() Ⅰ
Ⅰ![]() 求數(shù)列
求數(shù)列![]() 和數(shù)列
和數(shù)列![]() 的通項公式;
的通項公式;
![]() Ⅱ
Ⅱ![]() 令
令![]() ,若
,若![]() 對于一切的正整數(shù)
對于一切的正整數(shù)![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍;
的取值范圍;
![]() Ⅲ
Ⅲ![]() 數(shù)列
數(shù)列![]() 中是否存在
中是否存在![]() ,且
,且 ![]() 使
使![]() ,
,![]() ,
,![]() 成等差數(shù)列?若存在,求出
成等差數(shù)列?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,(其中
,(其中![]() ),
),![]() .
.
(1)若![]() 對定義域內(nèi)的任意實數(shù)x恒成立,求實數(shù)a的取值范圍;
對定義域內(nèi)的任意實數(shù)x恒成立,求實數(shù)a的取值范圍;
(2)若![]() 有兩個極值點
有兩個極值點![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)離心率為 ![]() 的橢圓
的橢圓![]() 的左、右焦點為
的左、右焦點為![]() , 點P是E上一點,
, 點P是E上一點, ![]() ,
, ![]() 內(nèi)切圓的半徑為
內(nèi)切圓的半徑為 ![]() .
.
(1)求E的方程;
(2)矩形ABCD的兩頂點C、D在直線![]() 上,A、B在橢圓E上,若矩形ABCD的周長為
上,A、B在橢圓E上,若矩形ABCD的周長為 ![]() , 求直線AB的方程.
, 求直線AB的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
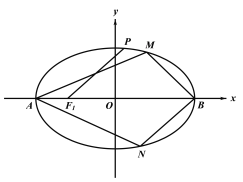
【題目】已知橢圓![]() 的左焦點為
的左焦點為![]() ,點
,點![]() 為橢圓的左、右頂點,點
為橢圓的左、右頂點,點![]() 是橢圓上一點,且直線
是橢圓上一點,且直線![]() 的傾斜角為
的傾斜角為![]() ,
,![]() ,已知橢圓的離心率為
,已知橢圓的離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)![]() 為橢圓上異于
為橢圓上異于![]() 的兩點,若直線
的兩點,若直線![]() 的斜率等于直線
的斜率等于直線![]() 斜率的
斜率的![]() 倍,求四邊形
倍,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】CPI是居民消費價格指數(shù)(consumer price index)的簡稱.居民消費價格指數(shù)是一個反映居民家庭一般所購買的消費品價格水平變動情況的宏觀經(jīng)濟指標(biāo).如圖是根據(jù)國家統(tǒng)計局發(fā)布的2017年6月—2018年6月我國CPI漲跌幅數(shù)據(jù)繪制的折線圖(注:2018年6月與2017年6月相比較,叫同比;2018年6月與2018年5月相比較,叫環(huán)比),根據(jù)該折線圖,則下列結(jié)論錯誤的是( )
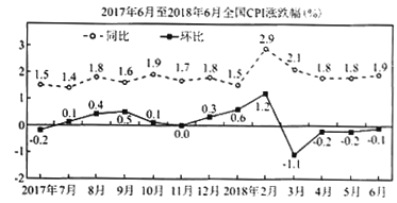
A.2017年8月與同年12月相比較,8月環(huán)比更大
B.2018年1月至6月各月與2017年同期相比較,CPI只漲不跌
C.2018年1月至2018年6月CPI有漲有跌
D.2018年3月以來,CPI在緩慢增長
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】關(guān)于函數(shù)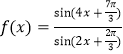 ,下列判斷正確的是( )
,下列判斷正確的是( )
A. ![]() 有最大值和最小值
有最大值和最小值
B. ![]() 的圖象的對稱中心為
的圖象的對稱中心為![]() (
(![]() )
)
C. ![]() 在
在![]() 上存在單調(diào)遞減區(qū)間
上存在單調(diào)遞減區(qū)間
D. ![]() 的圖象可由
的圖象可由![]() 的圖象向左平移
的圖象向左平移![]() 個單位而得
個單位而得
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如下面左圖,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,點
,點![]() 在
在![]() 上,且
上,且![]() ,將
,將![]() 沿
沿![]() 折起,得到四棱錐
折起,得到四棱錐![]() (如下面右圖).
(如下面右圖).
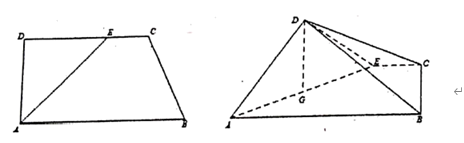
(1)求四棱錐![]() 的體積的最大值;
的體積的最大值;
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com