
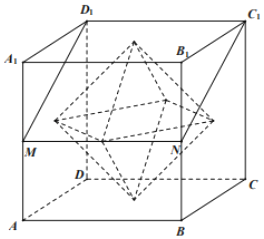
【題目】如圖,點M,N分別為正方體ABCD﹣A1B1C1D1的棱AA1,BB1的中點,以正方體的六個面的中心為頂點構成一個八面體,若平面D1MNC1將該八面體分割成上、下兩部分的體積分別為V1、V2,則![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
如圖,先作出平面![]() 截八面體的截面為
截八面體的截面為![]() ,建立空間直角坐標系,用點
,建立空間直角坐標系,用點![]() 到平面
到平面![]() 的距離
的距離![]() 為向量
為向量![]() 在法向量
在法向量![]() 上的投影的長,再計算兩部分的體積,得到體積之比,得到答案.
上的投影的長,再計算兩部分的體積,得到體積之比,得到答案.
正方體的六個面的中心為頂點構成的八面體中中間和上方的頂點分別為![]()
如圖,分別過![]() 作側棱的平行線,
作側棱的平行線,
分別![]() 交于點
交于點![]() ,分別
,分別![]() 交于點
交于點![]() ,得到矩形
,得到矩形![]() .
.

由題意有![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 的中點.
的中點.
在矩形![]() 中,
中,![]() 分別交
分別交![]() 于點
于點![]() ,則
,則![]() 分別為
分別為![]() 的中點,
的中點,
![]() 平面
平面![]() ,所以,
,所以,![]() 平面
平面![]() .
.
將平面![]() 延展與
延展與![]() 交于
交于![]() 點. 所以平面
點. 所以平面![]() 截八面體的截面為
截八面體的截面為![]() .
.
顯然![]() 與
與![]() 相交于
相交于![]() 的中點,設為
的中點,設為![]() .則
.則![]() 三點共線.
三點共線.
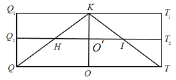
在![]() 中,過
中,過![]() 作
作![]() ,如圖,可得
,如圖,可得![]() 為
為![]() 的一個三等分點.
的一個三等分點.

設正方體的棱長為2,則![]() .
.
以![]() 為原點,
為原點,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,建立空間直角坐標系
軸,建立空間直角坐標系
P(-1,0,0),R(1,0,0),Q(0,-1,0),
![]()
![]()
![]()
設平面![]() 的法向量為
的法向量為![]() .
.
則 ,即
,即 ,取
,取![]() 則
則![]()
則點![]() 到平面
到平面![]() 的距離
的距離![]() 為向量
為向量![]() 在法向量
在法向量![]() 上的投影的長.
上的投影的長.
所以
又![]()

![]()
![]()
所以八面體在平面平面![]() 下方的部分的體積為
下方的部分的體積為![]()
所以![]()
故選:A



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn,且an=![]() (3n+Sn)對一切正整數n成立
(3n+Sn)對一切正整數n成立
(I)證明:數列{3+an}是等比數列,并求出數列{an}的通項公式;
(II)設![]() ,求數列
,求數列![]() 的前n項和Bn;
的前n項和Bn;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,圓![]() .以極點
.以極點![]() 為原點,極軸為
為原點,極軸為![]() 軸正半軸建立直角坐標系
軸正半軸建立直角坐標系![]() ,直線
,直線![]() 經過點
經過點![]() 且傾斜角為
且傾斜角為![]() .
.
![]() 求圓
求圓![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的參數方程;
的參數方程;
![]() 已知直線
已知直線![]() 與圓
與圓![]() 交與
交與![]() ,
,![]() ,滿足
,滿足![]() 為
為![]() 的中點,求
的中點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班要從6名男生4名女生中選出5人擔任5門不同學科的課代表,請分別求出滿足下列條件的方法種數![]() 結果用數字作答
結果用數字作答![]() .
.
(1)所安排的男生人數不少于女生人數;
(2)男生甲必須是課代表,但不能擔任語文課代表;
(3)女生乙必須擔任數學課代表,且男生甲必須擔任課代表,但不能擔任語文課代表.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|y=lg(x-![]() )},B={x|
)},B={x|![]() -cx<0,c>0},若AB,則實數c的取值范圍是( )
-cx<0,c>0},若AB,則實數c的取值范圍是( )
A.(0,1]B.[1,+∞)
C.(0,1)D.(1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,過拋物線C:y2=2px(p>0)的準線l上的點M(﹣1,0)的直線l1交拋物線C于A,B兩點,線段AB的中點為P.
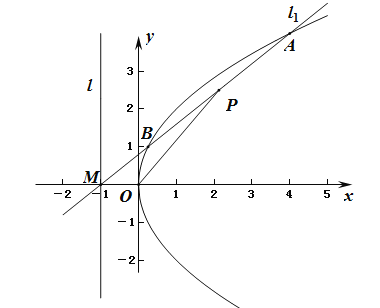
(Ⅰ)求拋物線C的方程;
(Ⅱ)若|MA||MB|=λ|OP|2,求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 已知函數f(x)=|x+a|+|x-2|.
(1)當a=-3時,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空間四邊形ABCD的對棱AD,BC成60°的角,且AD=a,BC=b,平行于AD與BC的截面分別交AB,AC,CD,BD于E、F、G、H,則截面EFGH面積的最大值為_____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com