Question

【題目】某商店為了更好地規劃某種商品進貨的量，該商店從某一年的銷售數據中，隨機抽取了組數據作為研究對象，如下圖所示（（噸）為該商品進貨量， （天）為銷售天數）：

	2	3	4	5	6	8	9	11
	1	2	3	3	4	5	6	8

（Ⅰ）根據上表數據在下列網格中繪制散點圖；

（Ⅱ）根據上表提供的數據，求出關于的線性回歸方程；

（Ⅲ)在該商品進貨量（噸）不超過6（噸）的前提下任取兩個值，求該商品進貨量x（噸）恰有一個值不超過3（噸）的概率.

參考公式和數據：，．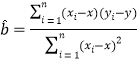

Answer 1

【答案】（Ⅰ）見解析（Ⅱ）（Ⅲ)

【解析】

（Ⅰ）在平面直角坐標系中畫出對應的散點圖即可．

（Ⅱ）根據公式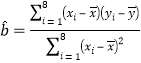先計算，再根據得到．

（Ⅲ)通過枚舉法可得基本事件的總數，從而得到隨機事件“該商品進貨量x（噸）恰有一個值不超過3（噸）”所含的基本事件數，由古典概型的概率公式即可得到答案．

（Ⅰ）散點圖如圖所示：

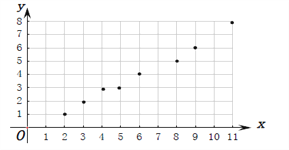
（Ⅱ）依題意，，

．

，

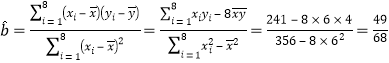故，回歸直線方程為．

（Ⅲ）由題意知，在該商品進貨量不超過6噸共有5個，設為編碼1，2，3，4，5號，任取兩個有（1，2）（1，3）（1，4）（1，5）（2，3）（2，4）（2，5）（3，4）（3，5）（4，5）共10種，該商品進貨量不超過3噸的有編號1，2號，超過3噸的是編號3，4，5號，該商品進貨量恰有一次不超過3噸有（1,3）（1,4）（1,5）（2,3）（2,4）(2,5)共6種，故該商品進貨量恰有一次不超過3噸的概率為．