
【題目】某校為評估新教改對教學的影響,挑選了水平相當的兩個平行班進行對比試驗.甲班采用創新教法,乙班仍采用傳統教法,一段時間后進行水平測試,成績結果全部落在[60,100]區間內(滿分100分),并繪制頻率分布直方圖如圖,兩個班人數均為60人,成績80分及以上為優良. 
(1)根據以上信息填好下列2×2聯表,并判斷出有多大的把握認為學生成績優良與班級有關?
是否優良 | 優良(人數) | 非優良(人數) | 合計 |
甲 | |||
乙 | |||
合計 |
(2)以班級分層抽樣,抽取成績優良的5人參加座談,現從5人中隨機選2人來作書面發言,求2人都來自甲班的概率. 下面的臨界值表供參考:
P(x2k) | 0.10 | 0.05 | 0.010 |
k | 2.706 | 3.841 | 6.635 |
(以下臨界值及公式僅供參考 ![]() ,n=a+b+c+d)
,n=a+b+c+d)
【答案】
(1)解:根據題意,填寫2×2列聯表如下;
是否優良 班級 | 優良 (人數) | 非優良 (人數) | 合計 |
甲 | 30 | 30 | 60 |
乙 | 20 | 40 | 60 |
合計 | 50 | 70 | 120 |
計算 ![]() ,
,
則有90%的把握認為學生成績優良與班級有關
(2)解:分層抽樣甲班抽取了3人,記作a1,a2,a3,乙班抽取了2人,記作b1,b2,
從中任意抽取2人,有{a1,a2},{a1,a3},{a1,b1},{a1,b2},
{a2,a3},{a2,b1},{a2,b2},{a3,b1},{a3,b2},{b1,b2}10種情形,
其中2人都來自甲班的有3種情形,
則至少有2人來自甲班的概率為P= ![]()
【解析】(1)根據所給數據可得列聯表,利用公式計算K2的值,對照臨界值即可得結論;(2)利用分層抽樣原理與列舉法計算基本事件數,求出對應的概率值.


科目:高中數學 來源: 題型:
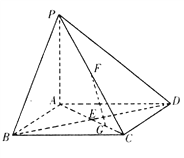
【題目】如圖,在底面是正方形的四棱錐![]() 面ABCD,BD交AC于點E,F是PC中點,G為AC上一點.
面ABCD,BD交AC于點E,F是PC中點,G為AC上一點.
(1)求證:![]() ;
;
(2)確定點G在線段AC上的位置,使FG//平面PBD,并說明理由;
(3)當二面角![]() 的大小為
的大小為![]() 時,求PC與底面ABCD所成角的正切值.
時,求PC與底面ABCD所成角的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖象過點
的圖象過點![]() .
.
(1)求![]() 的值并求函數
的值并求函數![]() 的值域;
的值域;
(2)若關于![]() 的方程
的方程![]() 有實根,求實數
有實根,求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() ,則是否存在實數
,則是否存在實數![]() ,使得函數
,使得函數![]() 的最大值為
的最大值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的偶函數,且當
上的偶函數,且當![]() 時,
時, ![]() .現已畫出函數
.現已畫出函數![]() 在
在![]() 軸左側的圖象,如圖所示,請根據圖象.
軸左側的圖象,如圖所示,請根據圖象.
(![]() )寫出函數
)寫出函數![]() 的增區間.
的增區間.
(![]() )寫出函數
)寫出函數![]() 的解析式.
的解析式.
(![]() )若函數
)若函數![]() ,求函數
,求函數![]() 的最小值.
的最小值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在R上的偶函數f(x)滿足:對任意的x1 , x2∈(﹣∞,0),有 ![]() ,則( )
,則( )
A.f(﹣4)<f(3)<f(﹣2)
B.f(﹣2)<f(3)<f(﹣4)
C.f(3)<f(﹣2)<f(﹣4)
D.f(﹣4)<f(﹣2)<f(3)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某城市氣象部門的數據中,隨機抽取了100天的空氣質量指數的監測數據如表:
空氣質量指數t | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | (300,+∞) |
質量等級 | 優 | 良 | 輕微污染 | 輕度污染 | 中度污染 | 嚴重污染 |
天數K | 5 | 23 | 22 | 25 | 15 | 10 |
(1)在該城市各醫院每天收治上呼吸道病癥總人數y與當天的空氣質量t(t取整數)存在如下關系y= ![]() ,且當t>300時,y>500估計在某一醫院收治此類病癥人數超過200人的概率;
,且當t>300時,y>500估計在某一醫院收治此類病癥人數超過200人的概率;
(2)若在(1)中,當t>300時,y與t的關系擬合于曲線 ![]() ,現已取出了10對樣本數據(ti , yi)(i=1,2,3,…,10),且
,現已取出了10對樣本數據(ti , yi)(i=1,2,3,…,10),且 ![]() =42500,
=42500, ![]() =500,求擬合曲線方程. (附:線性回歸方程
=500,求擬合曲線方程. (附:線性回歸方程 ![]() =a+bx中,b=
=a+bx中,b= ![]() ,a=
,a= ![]() ﹣b
﹣b ![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com