
【題目】【2018屆天津市耀華中學高三上學期第三次月考】已知橢圓![]() 的一個焦點在直線
的一個焦點在直線![]() 上,且離心率
上,且離心率![]() .
.
(1)求該橢圓的方程;
(2)若![]() 與
與![]() 是該橢圓上不同的兩點,且線段
是該橢圓上不同的兩點,且線段![]() 的中點
的中點![]() 在直線
在直線![]() 上,試證:
上,試證: ![]() 軸上存在定點
軸上存在定點![]() ,對于所有滿足條件的
,對于所有滿足條件的![]() 與
與![]() ,恒有
,恒有![]() ;
;
(3)在(2)的條件下, ![]() 能否為等腰直角三角形?并證明你的結論.
能否為等腰直角三角形?并證明你的結論.
【答案】(1)![]() (2)見解析(3)見解析
(2)見解析(3)見解析
【解析】試題分析: ![]() 利用橢圓的性質,離心率計算公式
利用橢圓的性質,離心率計算公式![]() 及
及![]() 即可求出;
即可求出;
⑵分直線![]() 的斜率存在與不存在兩種情況:
的斜率存在與不存在兩種情況: ![]() 斜率存在時,設出其方程,與橢圓方程聯立得到關于斜率的方程式,從而得到
斜率存在時,設出其方程,與橢圓方程聯立得到關于斜率的方程式,從而得到![]() 坐標間的關系式。假設
坐標間的關系式。假設![]() 軸上存在定點
軸上存在定點![]() ,對于所有滿足條件的
,對于所有滿足條件的![]() ,恒有
,恒有![]() ,得到點
,得到點![]() 的坐標,即證命題存在;當直線
的坐標,即證命題存在;當直線![]() 的斜率不存在時,易知
的斜率不存在時,易知![]() 成立,命題得證;
成立,命題得證;
⑶分類討論,利用等腰直角三角形的性質和兩點間的距離關系及其根與系數的關系即可得到滿足條件的直線斜率![]() 存在即可;
存在即可;
解析:(1)∵橢圓![]() 的一個焦點在直線
的一個焦點在直線![]() 上,∴
上,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴該橢圓的方程為![]() .
.
(2)當直線![]() 的斜率存在時,設直線
的斜率存在時,設直線![]() 的方程為
的方程為![]() ,
,
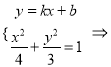
![]() ,
,
![]() ,
,
設![]() ,則
,則![]() ,
, ![]() ,
,
∵弦![]() 的中點
的中點![]() 在直線
在直線![]() 上,∴
上,∴![]()
![]() ,
,
∴![]()
![]() ,∴
,∴![]() ,
,
將![]() 代入
代入![]() 得
得![]() ,
,
假設在![]() 軸上存在定點
軸上存在定點![]() ,
, ![]()
![]() ,
,
∴![]()
![]()
![]() ,
,
∴![]()
![]() ,即
,即![]() ,
,
當直線![]() 的斜率不存在時,直線
的斜率不存在時,直線![]() 垂直于
垂直于![]() 軸,此時
軸,此時![]() 顯然成立,綜上,
顯然成立,綜上, ![]() 軸上存在定點
軸上存在定點![]() .
.
(3)假設![]() 能為等腰直角三角形,則
能為等腰直角三角形,則![]() ,
,
∴![]() ,
,
![]() ,
,
![]()
![]() ,
,
又![]() ,
,
∴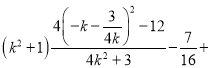
![]() ,
,
![]()
![]() ,符合(*),
,符合(*),
∴在(2)的條件下, ![]() 能為等腰直角三角形.
能為等腰直角三角形.


科目:高中數學 來源: 題型:
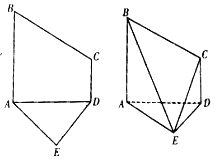
【題目】已知五邊形![]() 是由直角梯形
是由直角梯形![]() 和等腰直角三角形
和等腰直角三角形![]() 構成,如圖所示,
構成,如圖所示, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,將五邊形
,將五邊形![]() 沿著
沿著![]() 折起,且使平面
折起,且使平面![]() 平面
平面![]() .
.
(Ⅰ)若![]() 為
為![]() 中點,邊
中點,邊![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,說明理由;
的值;若不存在,說明理由;
(Ⅱ)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
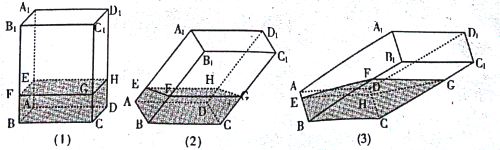
【題目】如圖,透明塑料制成的長方體ABCD﹣A1B1C1D1內灌進一些水,固定容器底面一邊BC于水平地面上,再將容器傾斜,隨著傾斜度不同,有下面五個命題:
①有水的部分始終呈棱柱形;
②沒有水的部分始終呈棱柱形;
③水面EFGH所在四邊形的面積為定值;
④棱A1D1始終與水面所在平面平行;
⑤當容器傾斜如圖(3)所示時,BEBF是定值.
其中所有正確命題的序號是 ____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓:![]() 的四個頂點圍成的四邊形的面積為
的四個頂點圍成的四邊形的面積為![]() ,原點到直線
,原點到直線![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知定點![]() ,是否存在過
,是否存在過![]() 的直線
的直線![]() ,使
,使![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且以
兩點,且以![]() 為直徑的圓過橢圓
為直徑的圓過橢圓![]() 的左頂點?若存在,求出
的左頂點?若存在,求出![]() 的方程:若不存在,請說明理由.
的方程:若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
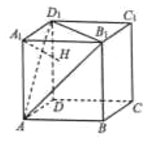
【題目】如圖,在正方體![]() 中,
中,![]() 平面
平面![]() ,垂足為H,給出下面結論:
,垂足為H,給出下面結論:
①直線![]() 與該正方體各棱所成角相等;
與該正方體各棱所成角相等;
②直線![]() 與該正方體各面所成角相等;
與該正方體各面所成角相等;
③過直線![]() 的平面截該正方體所得截面為平行四邊形;
的平面截該正方體所得截面為平行四邊形;
④垂直于直線![]() 的平面截該正方體,所得截面可能為五邊形,
的平面截該正方體,所得截面可能為五邊形,
其中正確結論的序號為( )
A. ①③ B. ②④ C. ①②④ D. ①②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為研究某種圖書每冊的成本費![]() (元)與印刷數
(元)與印刷數![]() (千冊)的關系,收集了一些數據并作了初步處理,得到了下面的散點圖及一些統計量的值.
(千冊)的關系,收集了一些數據并作了初步處理,得到了下面的散點圖及一些統計量的值.


表中![]() ,
, ![]() .
.
(1)根據散點圖判斷: ![]() 與
與![]() 哪一個更適宜作為每冊成本費
哪一個更適宜作為每冊成本費![]() (元)與印刷數
(元)與印刷數![]() (千冊)的回歸方程類型?(只要求給出判斷,不必說明理由)
(千冊)的回歸方程類型?(只要求給出判斷,不必說明理由)
(2)根據(1)的判斷結果及表中數據,建立![]() 關于
關于![]() 的回歸方程(回歸系數的結果精確到0.01);
的回歸方程(回歸系數的結果精確到0.01);
(3)若每冊書定價為10元,則至少應該印刷多少千冊才能使銷售利潤不低于78840元?(假設能夠全部售出,結果精確到1)
(附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ,
, ![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com