
【題目】為了研究某種藥物,用小白鼠進行試驗,發現藥物在血液內的濃度與時間的關系因使用方式的不同而不同。若使用注射方式給藥,則在注射后的3小時內,藥物在白鼠血液內的濃度![]() 與時間t滿足關系式:
與時間t滿足關系式:![]() ,若使用口服方式給藥,則藥物在白鼠血液內的濃度
,若使用口服方式給藥,則藥物在白鼠血液內的濃度![]() 與時間t滿足關系式:
與時間t滿足關系式: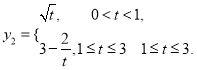 現對小白鼠同時進行注射和口服該種藥物,且注射藥物和口服藥物的吸收與代謝互不干擾。
現對小白鼠同時進行注射和口服該種藥物,且注射藥物和口服藥物的吸收與代謝互不干擾。
(1)若a=1,求3小時內,該小白鼠何時血液中藥物的濃度最高,并求出最大值?
(2)若使小白鼠在用藥后3小時內血液中的藥物濃度不低于4,求正數a的取值范圍。
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() +
+![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為![]() ,直線l:x+2y=4與橢圓有且只有一個交點T.
,直線l:x+2y=4與橢圓有且只有一個交點T.
(I)求橢圓C的方程和點T的坐標;
(Ⅱ)O為坐標原點,與OT平行的直線l′與橢圓C交于不同的兩點A,B,直線l′與直線l交于點P,試判斷![]() 是否為定值,若是請求出定值,若不是請說明理由.
是否為定值,若是請求出定值,若不是請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解一家企業生產的某類產品的使用壽命(單位:小時),現從中隨機抽取一定數量的產品進行測試,繪制頻率分布直方圖如圖所示.

(1)假設同一組中的每個數據可用該組區間的中點值代替,估算這批產品的平均使用壽命;
(2)已知該企業生產的這類產品有甲、乙兩個系列,產品使用壽命不低于60小時為合格,合格產品中不低于90小時為優異,其余為一般.現從合格產品中,用分層抽樣的方法抽取70件,其中甲系列有35件(1件優異).請完成下面的列聯表,并根據列聯表判斷能否有![]() 的把握認為產品優異與系列有關?
的把握認為產品優異與系列有關?
甲系列 | 乙系列 | 合計 | |
優異 | |||
一般 | |||
合計 |
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
參考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
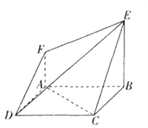
【題目】如圖,在空間幾何體ABCDFE中,底面![]() 是邊長為2的正方形,
是邊長為2的正方形,![]() ,
,![]() ,
,![]() .
.
(1)求證:AC//平面DEF;
(2)已知![]() ,若在平面
,若在平面![]() 上存在點
上存在點![]() ,使得
,使得![]() 平面
平面![]() ,試確定點
,試確定點![]() 的位置.
的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() ,且離心率為
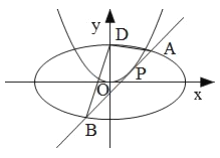
,且離心率為![]() .過拋物線
.過拋物線![]() 上一點
上一點![]() 作
作![]() 的切線
的切線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點.
兩點.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)是否存在直線![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“雙十一網購狂歡節”源于淘寶商城(天貓)2009年11月11日舉辦的促銷活動,當時參與的商家數量和促銷力度均有限,但營業額遠超預想的效果,于是11月11日成為天貓舉辦大規模促銷活動的固定日期.如今,中國的“雙十一”已經從一個節日變成了全民狂歡的“電商購物日”.某淘寶電商為分析近8年“雙十一”期間的宣傳費用![]() (單位:萬元)和利潤
(單位:萬元)和利潤![]() (單位:十萬元)之間的關系,搜集了相關數據,得到下列表格:
(單位:十萬元)之間的關系,搜集了相關數據,得到下列表格:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)請用相關系數![]() 說明
說明![]() 與
與![]() 之間是否存在線性相關關系(當
之間是否存在線性相關關系(當![]() 時,說明
時,說明![]() 與
與![]() 之間具有線性相關關系);
之間具有線性相關關系);
(2)建立![]() 關于
關于![]() 的線性回歸方程(系數精確到
的線性回歸方程(系數精確到![]() ),預測當宣傳費用為
),預測當宣傳費用為![]() 萬元時的利潤,
萬元時的利潤,
附參考公式:回歸方程![]() 中
中![]() 和
和![]() 最小二乘估計公式分別為
最小二乘估計公式分別為
 ,
,![]() ,相關系數
,相關系數
參考數據:
![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】公交車的數量太多容易造成資源浪費,太少又難以滿足乘客的需求,為了合理布置車輛,公交公司在2路車的乘客中隨機調查了50名乘客,經整理,他們候車時間(單位:![]() )的莖葉圖如下:
)的莖葉圖如下:

(Ⅰ)將候車時間分為![]() 八組,作出相應的頻率分布直方圖;
八組,作出相應的頻率分布直方圖;

(Ⅱ)若公交公司將2路車發車時間調整為每隔15![]() 發一趟車,那么上述樣本點將發生變化(例如候車時間為9
發一趟車,那么上述樣本點將發生變化(例如候車時間為9![]() 的不變,候車時間為17
的不變,候車時間為17![]() 的變為2
的變為2![]() ),現從2路車的乘客中任取5人,設其中候車時間不超過10
),現從2路車的乘客中任取5人,設其中候車時間不超過10![]() 的乘客人數為
的乘客人數為![]() ,求
,求![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·北京高考)由四棱柱ABCDA1B1C1D1截去三棱錐C1B1CD1后得到的幾何體如圖所示.四邊形ABCD為正方形,O為AC與BD的交點,E為AD的中點,A1E⊥平面ABCD.
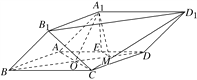
(1)證明:A1O∥平面B1CD1;
(2)設M是OD的中點,證明:平面A1EM⊥平面B1CD1.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com