
已知函數 ,的部分圖象如圖所示.
,的部分圖象如圖所示.
(Ⅰ)求函數 的解析式;
的解析式;
(Ⅱ)求函數 的單調遞增區間.
的單調遞增區間.
(Ⅰ)f (x)=2sin(2x+ );(Ⅱ)
);(Ⅱ) (k∈Z).
(k∈Z).
解析試題分析:(Ⅰ)根據圖像與x軸的交點可求得 ,進而求得
,進而求得 ;然后根據函數圖像過點(
;然后根據函數圖像過點( ,0)可得
,0)可得 ,過點(0,1)可得A=2,即可求得解析式f (x)=2sin(2x+
,過點(0,1)可得A=2,即可求得解析式f (x)=2sin(2x+ );(Ⅱ)用換元法即可求得g(x)的單調遞增區間是
);(Ⅱ)用換元法即可求得g(x)的單調遞增區間是 (k∈Z).
(k∈Z).
試題解析:(Ⅰ)由題設圖象知,周期 ,所以
,所以 ,
,
因為點( ,0)在函數圖象上,所以Asin(2×
,0)在函數圖象上,所以Asin(2× +φ)=0,即sin(
+φ)=0,即sin( +φ)=0.
+φ)=0.
又因為0<φ<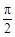 ,所以
,所以 ,從而
,從而 +φ=π,即
+φ=π,即 .
.
又點(0,1)在函數圖象上,所以 ,得A=2,
,得A=2,
故函數f (x)的解析式為f (x)=2sin(2x+ ).
).
(Ⅱ)由 ,
,
得 ,k∈Z,
,k∈Z,
所以函數g(x)的單調遞增區間是 (k∈Z).
(k∈Z).
考點:1.正弦型函數解析式的求法;2.三角函數的單調性.


 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com