
【題目】已知橢圓 ![]() 的左、右焦點分別為
的左、右焦點分別為 ![]() ,橢圓
,橢圓 ![]() 過點
過點 ![]() ,直線
,直線 ![]() 交
交 ![]() 軸于
軸于 ![]() ,且
,且 ![]() ,
, ![]() 為坐標原點.
為坐標原點.
(1)求橢圓 ![]() 的方程;
的方程;
(2)設 ![]() 是橢圓
是橢圓 ![]() 的上頂點,過點
的上頂點,過點 ![]() 分別作直線
分別作直線 ![]() 交橢圓
交橢圓 ![]() 于
于 ![]() 兩點,設這兩條直線的斜率分別為
兩點,設這兩條直線的斜率分別為 ![]() ,且
,且 ![]() ,證明:直線
,證明:直線 ![]() 過定點.
過定點.
科目:高中數學 來源: 題型:
【題目】已知中心在原點的橢圓C的左焦點F(﹣ ![]() ,0),右頂點A(2,0).
,0),右頂點A(2,0).
(1)求橢圓C的標準方程;
(2)斜率為 ![]() 的直線l與橢圓C交于A、B兩點,求弦長|AB|的最大值及此時l的直線方程.
的直線l與橢圓C交于A、B兩點,求弦長|AB|的最大值及此時l的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司一年需購買某種原料600噸,設公司每次都購買![]() 噸,每次運費為3萬元,一年的總存儲費為
噸,每次運費為3萬元,一年的總存儲費為![]() 萬元,一年的總運費與總存儲費之和為
萬元,一年的總運費與總存儲費之和為![]() (單位:萬元).
(單位:萬元).
(1)試用解析式得![]() 表示成
表示成![]() 的函數;
的函數;
(2)當![]() 為何值時,
為何值時, ![]() 取得最小值?并求出
取得最小值?并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖, ![]() 是邊長為
是邊長為 ![]() 的正方形,
的正方形, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 與平面
與平面 ![]() 所成角為
所成角為 ![]() .
.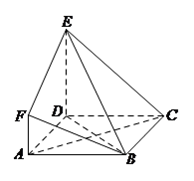
(Ⅰ)求證: ![]() 平面
平面 ![]() .
.
(Ⅱ)求二面角 ![]() 的余弦值.
的余弦值.
(Ⅲ)設點 ![]() 是線段
是線段 ![]() 上一個動點,試確定點
上一個動點,試確定點 ![]() 的位置,使得
的位置,使得 ![]() 平面
平面 ![]() ,并證明你的結論.
,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 且滿足Sn=2an﹣2;數列{bn}的前n項和為Tn , 且滿足b1=1,b2=2, ![]() .
.
(1)求數列{an}、{bn}的通項公式;
(2)是否存在正整數n,使得 ![]() 恰為數列{bn}中的一項?若存在,求所有滿足要求的bn;若不存在,說明理由.
恰為數列{bn}中的一項?若存在,求所有滿足要求的bn;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了綠化城市,要在矩形區域ABCD內建一個矩形草坪,如圖所示,另外,△AEF內部有一文物保護區不能占用,經測量AB=100 m,BC=80 m,AE=30 m,AF=20 m,應如何設計才能使草坪面積最大?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com