本試題主要是考查了不等式的證明,利用均值不等式和消元的思想,表示參數,然后結合
a,
b是方程
x2-(1-
c)
x+
c2-
c=0的兩個不等實根,得到判別式大于零,得到c的范圍。
因為
a+
b=1-
c,
ab=
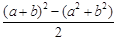
=
c2-
c, ………………………3分
所以
a,
b是方程
x2-(1-
c)
x+
c2-
c=0的兩個不等實根,
則△=(1-
c)
2-4(
c2-
c)>0,得-
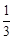
<
c<1, ………………………5分
而(
c-
a)(
c-b)=
c2-(
a+
b)
c+
ab>0,
即
c2-(1-
c)
c+
c2-
c>0,得
c<0,或
c>
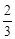
, …………………………8分
又因為
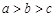
,所以
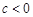
.所以-
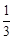
<
c<0,即1<
a+
b<
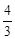
. …………10分

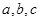 滿足
滿足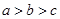 ,且
,且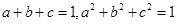 ,求證:
,求證: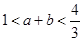
 名校課堂系列答案
名校課堂系列答案