
(14分)如圖,在四棱錐![]() 中,
中,![]() ,
,
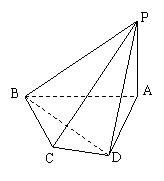
![]() ,BC⊥AB,CD⊥AD,BC=CD=PA=a,
,BC⊥AB,CD⊥AD,BC=CD=PA=a,
(Ⅰ)求證:平面PBD⊥平面PAC.
(Ⅱ)求四棱錐P-ABCD的體積V;
科目:高中數(shù)學(xué) 來源: 題型:
(08年安徽信息交流文)(本小題滿分14分)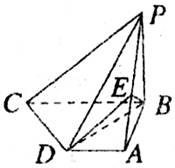 如圖,在四棱錐P-ABCD中,PB⊥底面
如圖,在四棱錐P-ABCD中,PB⊥底面![]() ,CD⊥PD,底面ABCD為直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,點E在棱PA上,且PE=2EA。
,CD⊥PD,底面ABCD為直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,點E在棱PA上,且PE=2EA。
(1)求二面角P-CD-B的正切值;
(2)求異面直線PA與CD所成的角;
(3)求證:PC∥平面EBD。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分14分)![]()
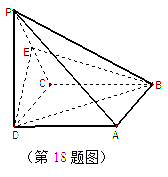 如圖,在四棱錐
如圖,在四棱錐![]() 中,底面
中,底面![]() 是正方形,側(cè)棱
是正方形,側(cè)棱![]() 底面
底面![]() ,
,![]() ,
,![]() 是
是![]() 的中點。
的中點。![]()
(1)證明:![]() ;
;![]()
(2)求![]() 以
以![]() 為軸旋轉(zhuǎn)所圍成的幾何體體積。
為軸旋轉(zhuǎn)所圍成的幾何體體積。![]()
![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本題滿分14分)如圖,在四棱錐![]() 中,
中,
底面![]() 是正方形,側(cè)面
是正方形,側(cè)面![]() 底面
底面![]() ,
,
且![]() ,若
,若![]() 、
、![]() 分別為
分別為![]() 、
、
![]() 的中
的中![]() 點.(Ⅰ) 求證:
點.(Ⅰ) 求證:![]() ∥平面
∥平面![]() ;
;
(Ⅱ) 求證:![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011學(xué)年江蘇省高三學(xué)情調(diào)研考試數(shù)學(xué)卷 題型:解答題
(本小題滿分14分)
如圖,在四棱錐P—ABCD中,AB∥CD,CD=2AB,AB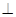 平面PAD,E為PC的中點.
平面PAD,E為PC的中點.
(1)求證:BE∥平面PAD;
(2)若AD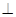 PB,求證:PA
PB,求證:PA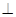 平面ABC D.
平面ABC D.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年廣東省高考沖刺強化訓(xùn)練試卷三文科數(shù)學(xué) 題型:解答題
(本小題滿分14分)如圖,在四棱錐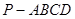 中,底面ABCD是正方形,側(cè)棱
中,底面ABCD是正方形,側(cè)棱 底面ABCD,
底面ABCD, ,E是PC的中點,作
,E是PC的中點,作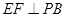 交PB于點F.
交PB于點F.
(I) 證明: PA∥平面EDB;
(II) 證明:PB⊥平面EFD;
(III) 求三棱錐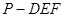 的體積.
的體積.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com