
【題目】有以下四種變換方式:
![]() 向左平移
向左平移![]() 個單位長度,再把所得各點的橫坐標縮短到原來的
個單位長度,再把所得各點的橫坐標縮短到原來的![]() 倍
倍![]() 縱坐標不變
縱坐標不變![]() ;
;
![]() 向左平移
向左平移![]() 個單位長度,再把所得各點的橫坐標縮短到原來的
個單位長度,再把所得各點的橫坐標縮短到原來的![]() 倍
倍![]() 縱坐標不變
縱坐標不變![]() ;
;
![]() 把各點的橫坐標縮短到原來的
把各點的橫坐標縮短到原來的![]() 倍
倍![]() 縱坐標不變
縱坐標不變![]() ,再向左平移
,再向左平移![]() 個單位長度;
個單位長度;
![]() 把各點的橫坐標縮短到原來的
把各點的橫坐標縮短到原來的![]() 倍
倍![]() 縱坐標不變
縱坐標不變![]() ,再向左平移
,再向左平移![]() 個單位長度;
個單位長度;
其中能將函數![]() 的圖象變為函數
的圖象變為函數![]() 的圖象的是
的圖象的是![]()
![]()
A. ![]() 和
和![]() B.
B. ![]() 和
和![]() C.
C. ![]() 和
和![]() D.
D. ![]() 和
和![]()
科目:高中數學 來源: 題型:
【題目】根據國家環保部最新修訂的《環境空氣質量標準》規定:居民區PM2.5的年平均濃度不得超過35微克/立方米,PM2.5的24小時平均濃度不得超過75微克/立方米。某城市環保部分隨機抽取的一居民區過去20天PM2.5的24小時平均濃度的監測數據,數據統計如下:
組別 | PM2.5平均濃度 | 頻數 | 頻率 |
第一組 | (0,25] | 3 | 0.15 |
第二組 | (25,50] | 12 | 0.6 |
第三組 | (50,75] | 3 | 0.15 |
第四組 | (75,100] | 2 | 0.1 |
(Ⅰ)從樣本中PM2.5的24小時平均濃度超過50微克/立方米的5天中,隨機抽取2天,求恰好有一天PM2.5的24小時平均濃度超過75微克/立方米的概率;
(II)求樣本平均數,并根據樣本估計總計的思想,從PM2.5的年平均濃度考慮,判斷該居民區的環境是否需要改進?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】必修四第一章我們借助圓的對稱性學習了誘導公式,如![]() 在直觀上講單位圓中,當兩個角的終邊關于
在直觀上講單位圓中,當兩個角的終邊關于![]() 軸對稱時,這兩個角的正弦值相等;再如
軸對稱時,這兩個角的正弦值相等;再如![]() 在單位圓中,當兩個角的終邊關于原點中心對稱時,這兩個角的正弦值互為相反數.觀察這些誘導公式,可以發現它們都是特殊角與任意角
在單位圓中,當兩個角的終邊關于原點中心對稱時,這兩個角的正弦值互為相反數.觀察這些誘導公式,可以發現它們都是特殊角與任意角![]() 的三角函數的恒等關系.我們如果將特殊角換為任意角
的三角函數的恒等關系.我們如果將特殊角換為任意角![]() ,那么任意角
,那么任意角![]() 與
與![]() 的和(或差)的三角函數與
的和(或差)的三角函數與![]() ,
,![]() 的三角函數會有什么關系呢?如果已知
的三角函數會有什么關系呢?如果已知![]() ,
,![]() 的正弦余弦,能由此推出
的正弦余弦,能由此推出![]() 的正弦余弦嗎?下面是某高一學生在老師的指導下自行探究
的正弦余弦嗎?下面是某高一學生在老師的指導下自行探究![]() 與角
與角![]()
![]() 的正弦余弦之間的關系的部分過程,請你順著這位同學的思路以及老師的提示將探究過程完善,并完成后面的題目.探究過程如下:
的正弦余弦之間的關系的部分過程,請你順著這位同學的思路以及老師的提示將探究過程完善,并完成后面的題目.探究過程如下:
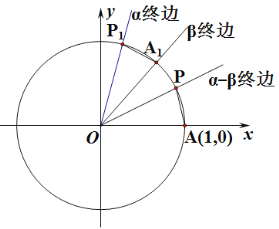
不妨令![]() 如圖,設單位圓與
如圖,設單位圓與![]() 軸的正半軸相交于點
軸的正半軸相交于點![]() 以
以![]() 軸的非負半軸為始邊作角
軸的非負半軸為始邊作角![]() 它們的終邊分別與單位圓相交于點
它們的終邊分別與單位圓相交于點![]() 連接
連接![]() 若把扇形
若把扇形![]() 繞著點
繞著點![]() 旋轉
旋轉![]() 角,則點
角,則點![]() 分別與點
分別與點![]() 重合. ……(未完待續)
重合. ……(未完待續)
(提示一:任意一個圓繞著其圓心旋轉任意角后都與原來的圓重合,這一性質叫做圓的旋轉對稱性)(提示二:平面上任意兩點![]() 間的距離公式
間的距離公式![]() )
)
(1)完善上述探究過程;
(2)利用(1)中的結論解決問題:已知![]()
![]() 是第三象限角,求
是第三象限角,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了估計某自然保護區中天鵝的數量,可以使用以下方法:先從該保護區中捕出一定數量的天鵝,例如200只,給每只天鵝做上不影響其存活的記號,然后放回保護區,經過適當的時間,讓其和保護區中其余的天鵝充分混合,再從保護區中捕出一定數量的天鵝,例如150只,查看其中有記號的天鵝,設有20只,試根據上述數據,估計該自然保護區中天鵝的數量.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】返鄉創業的大學生一直是人們比較關注的對象,他們從大學畢業,沒有選擇經濟發達的大城市,而是回到自己的家鄉,為養育自己的家鄉貢獻自己的力量,在享有“國際花園城市”稱號的溫江幸福田園,就有一個由大學畢業生創辦的農家院“小時代”,其獨特的裝修風格和經營模式,引來無數人的關注,帶來紅紅火火的現狀,給青年大學生們就業創業上很多新的啟示.在接受采訪中,該老板談起以下情況:初期投入為72萬元,經營后每年的總收入為50萬元,第n年需要付出房屋維護和工人工資等費用是首項為12,公差為4的等差數列![]() (單位:萬元).
(單位:萬元).
(1)求![]() ;
;
(2)該農家樂第幾年開始盈利?能盈利幾年?(即總收入減去成本及所有費用之差為正值)
(3)該農家樂經營多少年,其年平均獲利最大?年平均獲利的最大值是多少?(年平均獲利![]() 前
前![]() 年總獲利
年總獲利![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某盒子內裝有三種顏色的玻璃球,一位同學每次從中隨機拿出一個玻璃球,觀察顏色后再放回,重復了50次,得到的信息如下:觀察到紅色26次、藍色13次.如果從這個盒子內任意取一個玻璃球,估計:
(1)這個球既不是紅色也不是藍色的概率;
(2)這個球是紅色或者是藍色的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
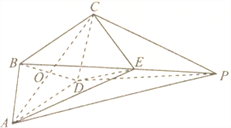
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的菱形,
的菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 與
與![]() 的交點,
的交點, ![]() 為棱
為棱![]() 上一點.
上一點.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,三棱錐
,三棱錐![]() 的體積為
的體積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com