Question

已知實數x滿足2x²≤3x，求函數f（x）=（k²+1）x²-2（k²+1）x+3（k∈R）的最小值和最大值．

Answer 1

【答案】分析：先由已知2x²≤3x，可得，即函數f（x）是定義在區間上的二次函數．再結合二次函數圖象開口向上，對稱軸方程x=1，利用二次函數的性質可知，函數f（x）的最小值和最大值．
解答：解：由已知2x²≤3x，可得，（4分）
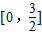
即函數f（x）是定義在區間上的二次函數．
因k²+1＞0，二次函數圖象開口向上，對稱軸方程x=1，
由二次函數的性質可知，
函數f（x）的最小值為f（1）=-k²+2，（8分）
最大值為f（0）=3．（12分）
點評：本小題考查解不等式、二次函數在區間上的最值問題．屬基礎題