
【題目】已知函數![]() .
.
(1)若函數![]() 在
在![]() 處取得極值,求曲線
處取得極值,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)討論函數![]() 的單調性;
的單調性;
(3)設![]() ,若
,若![]() 對
對![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)當
;(2)當![]() 時,
時,![]() 在
在![]() 上單調遞增,當
上單調遞增,當![]() 時,
時,![]() 在
在![]() 和
和![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,當
上單調遞減,當![]() 時,
時,![]() 在
在![]() 上單調遞減,
上單調遞減,![]() 上單調遞增;(3)
上單調遞增;(3) .
.
【解析】
試題分析:(1)先求![]() ,得
,得![]() 即為切線斜率,利用點斜式求解;(2)求出
即為切線斜率,利用點斜式求解;(2)求出![]() 的導數,通過討論
的導數,通過討論![]() 的范圍,確實導函數的符號, 從而求出函數的單調區間;(3)問題轉化為
的范圍,確實導函數的符號, 從而求出函數的單調區間;(3)問題轉化為![]() 對
對![]() 恒成立, 令
恒成立, 令![]() ,通過討論函數
,通過討論函數![]() 的單調性得到其最小值, 解關于
的單調性得到其最小值, 解關于![]() 的不等式即可求出
的不等式即可求出![]() 的范圍.
的范圍.
試題解析:(1)由![]() ,
,![]() ,得
,得![]() 或
或![]() (舍去)
(舍去)
經檢驗,當![]() 時,函數
時,函數![]() 在
在![]() 處取得極值.
處取得極值.
![]() 時,
時,![]() ,
,![]()
則![]() ,
,![]()
所以所求的切線方式為![]() ,整理得
,整理得![]() .
.
(2)![]() 定義域為
定義域為![]()
![]()
![]()
![]() ,
,
令![]() ,得
,得![]() 或
或![]()
∵![]() ,則
,則![]() ,且
,且![]()
①當![]() 時,
時,![]() ,
,![]() ,此時
,此時![]() 在
在![]() 上單調遞增;
上單調遞增;
②當![]() 時,
時,![]() 在
在![]() 和
和![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;
上單調遞減;
③當![]() 時,
時,![]() 在
在![]() 上單調遞減,
上單調遞減,![]() 上單調遞增.
上單調遞增.
(3)由題意,![]() ,
,
即![]() ,即
,即![]() 對任意
對任意![]() 恒成立,
恒成立,
令![]() ,則
,則![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() 在
在![]() 上單調遞減,
上單調遞減,![]() 上單調遞增,
上單調遞增,
當![]() 時
時![]() 取得最小值
取得最小值![]()
∴![]() ,解得
,解得![]()
又∵![]() ,所以
,所以![]() 的取值范圍為
的取值范圍為 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】設集合A={x|x2-3x<0},B={x|-2≤x≤2},則A∩B=( )
A. {x|2≤x<3} B. {x|-2≤x<0}
C. {x|0<x≤2} D. {x|-2≤x<3}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市為了制定合理的節水方案,對居民用水情況進行了調查,通過抽樣,獲得了某年![]() 位居民每人的月均用水量(單位:噸),將數據按照
位居民每人的月均用水量(單位:噸),將數據按照![]() 分成
分成![]() 組,制成了如圖所示的頻率分布直方圖.
組,制成了如圖所示的頻率分布直方圖.
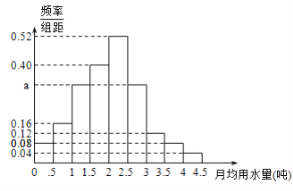
(1)求直方圖中的![]() 值;
值;
(2)設該市有![]() 萬居民,估計全市居民中月均用水量不低于
萬居民,估計全市居民中月均用水量不低于![]() 噸的人數.說明理由;
噸的人數.說明理由;
(3)估計居民月均用水量的中位數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以原點
中,以原點![]() 為極點,以
為極點,以![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的直角坐標方程并指出其形狀;
的直角坐標方程并指出其形狀;
(2)設![]() 是曲線
是曲線![]() 上的動點,求
上的動點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若P(2,-1)為圓(x-1)2+y2=25的弦AB的中點,則直線AB的方程是 ( )
A. x-y-3=0 B. 2x+y-3=0 C. x+y-1=0 D. 2x-y-5=0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個盒子中裝有紅、黃、藍三種顏色的球各5個,從中任取3個球.事件甲:3個球都不是紅球;事件乙:3個球不都是紅球;事件丙:3個球都是紅球;事件丁:3個球中至少有1個紅球,則下列選項中兩個事件互斥而不對立的是( )
A. 甲和乙 B. 甲和丙 C. 乙和丙 D. 乙和丁
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是一塊鍍鋅鐵皮的邊角料![]() ,其中
,其中![]() 都是線段,曲線段
都是線段,曲線段![]() 是拋物線的一部分,且點
是拋物線的一部分,且點![]() 是該拋物線的頂點,
是該拋物線的頂點,![]() 所在直線是該拋物線的對稱軸. 經測量,
所在直線是該拋物線的對稱軸. 經測量,![]() 2米,
2米,![]() 米,
米,![]() ,點
,點![]() 到
到![]() 的距離
的距離![]() 的長均為1米.現要用這塊邊角料裁一個矩形
的長均為1米.現要用這塊邊角料裁一個矩形![]() (其中點
(其中點![]() 在曲線段
在曲線段![]() 或線段
或線段![]() 上,點
上,點![]() 在線段
在線段![]() 上,點
上,點![]() 在線段
在線段![]() 上). 設
上). 設![]() 的長為
的長為![]() 米,矩形
米,矩形![]() 的面積為
的面積為![]() 平方米.
平方米.

(1)將![]() 表示為
表示為![]() 的函數;
的函數;
(2)當![]() 為多少米時,
為多少米時,![]() 取得最大值,最大值是多少?
取得最大值,最大值是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com