
【題目】點O是平面上一定點,A、B、C是平面上△ABC的三個頂點,∠B、∠C分別是邊AC、AB的對角,以下命題正確的是(把你認為正確的序號全部寫上). ①動點P滿足 ![]() =
= ![]() +
+ ![]() +
+ ![]() ,則△ABC的重心一定在滿足條件的P點集合中;
,則△ABC的重心一定在滿足條件的P點集合中;
②動點P滿足 ![]() =
= ![]() +λ(
+λ( ![]() +
+ ![]() )(λ>0),則△ABC的內心一定在滿足條件的P點集合中;
)(λ>0),則△ABC的內心一定在滿足條件的P點集合中;
③動點P滿足 ![]() =
= ![]() +λ(
+λ( 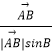 +
+ 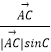 )(λ>0),則△ABC的重心一定在滿足條件的P點集合中;
)(λ>0),則△ABC的重心一定在滿足條件的P點集合中;
④動點P滿足 ![]() =
= ![]() +λ(
+λ( 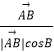 +
+ 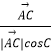 )(λ>0),則△ABC的垂心一定在滿足條件的P點集合中;
)(λ>0),則△ABC的垂心一定在滿足條件的P點集合中;
⑤動點P滿足 ![]() =
= ![]() +λ(
+λ( 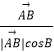 +
+ 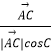 )(λ>0),則△ABC的外心一定在滿足條件的P點集合中.
)(λ>0),則△ABC的外心一定在滿足條件的P點集合中.
【答案】①②③④⑤
【解析】解:對于①,∵動點P滿足 ![]() =
= ![]() +
+ ![]() +
+ ![]() , ∴
, ∴ ![]() =
= ![]() +
+ ![]() ,
,
則點P是△ABC的重心,故①正確;
對于②,∵動點P滿足 ![]() =
= ![]() +λ(
+λ( ![]() +
+ ![]() )(λ>0),
)(λ>0),
∴ ![]() =λ(
=λ( ![]() +
+ ![]() )(λ>0),
)(λ>0),
又 ![]() +
+ ![]() 在∠BAC的平分線上,
在∠BAC的平分線上,
∴ ![]() 與∠BAC的平分線所在向量共線,
與∠BAC的平分線所在向量共線,
∴△ABC的內心在滿足條件的P點集合中,②正確;
對于③,動點P滿足 ![]() =
= ![]() +λ(
+λ( 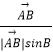 +
+ 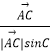 )(λ>0),
)(λ>0),
∴ ![]() =λ(
=λ( 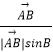 +
+ 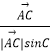 ),(λ>0),
),(λ>0),
過點A作AD⊥BC,垂足為D,則| ![]() |sinB=|
|sinB=| ![]() |sinC=AD,
|sinC=AD,![]() =
= ![]() (
( ![]() +
+ ![]() ),向量
),向量 ![]() +
+ ![]() 與BC邊的中線共線,
與BC邊的中線共線,
因此△ABC的重心一定在滿足條件的P點集合中,③正確;
對于④,動點P滿足 ![]() =
= ![]() +λ(
+λ( 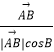 +
+ 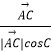 )(λ>0),
)(λ>0),
∴ ![]() =λ(
=λ( 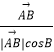 +
+ 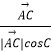 )(λ>0),
)(λ>0),
∴ ![]()
![]() =λ(
=λ( 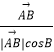 +
+ 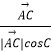 )
) ![]() =λ(|
=λ(| ![]() |﹣|
|﹣| ![]() |)=0,
|)=0,
∴ ![]() ⊥
⊥ ![]() ,
,
∴△ABC的垂心一定在滿足條件的P點集合中,④正確;
對于⑤,動點P滿足 ![]() =
= ![]() +λ(
+λ( 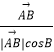 +
+ 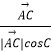 )(λ>0),
)(λ>0),
設 ![]() =
= ![]() ,
,
則 ![]() =λ(
=λ( 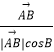 +
+ 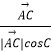 ),
),
由④知( 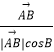 +
+ 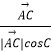 )
) ![]() =0,
=0,
∴ ![]()
![]() =0,
=0,
∴ ![]() ⊥
⊥ ![]() ,
,
∴P點的軌跡為過E的BC的垂線,即BC的中垂線;
∴△ABC的外心一定在滿足條件的P點集合,⑤正確.
故正確的命題是①②③④⑤.
所以答案是:①②③④⑤.
【考點精析】根據題目的已知條件,利用命題的真假判斷與應用的相關知識可以得到問題的答案,需要掌握兩個命題互為逆否命題,它們有相同的真假性;兩個命題為互逆命題或互否命題,它們的真假性沒有關系.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知a>0,設命題p:函數y=ax在R上單調遞增;命題q:不等式ax2﹣ax+1>0對x∈R恒成立,若p且q為假,p或q為真,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=sin(2x+ ![]() )+
)+ ![]() cos(2x+
cos(2x+ ![]() ),則( )
),則( )
A.y=f(x)在(0, ![]() )單調遞增,其圖象關于直線x=
)單調遞增,其圖象關于直線x= ![]() 對稱
對稱
B.y=f(x)在(0, ![]() )單調遞增,其圖象關于直線x=
)單調遞增,其圖象關于直線x= ![]() 對稱
對稱
C.y=f(x)在(0, ![]() )單調遞減,其圖象關于直線x=
)單調遞減,其圖象關于直線x= ![]() 對稱
對稱
D.y=f(x)在(0, ![]() )單調遞減,其圖象關于直線x=
)單調遞減,其圖象關于直線x= ![]() 對稱
對稱
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC是一個面積較大的三角形,點P是△ABC所在平面內一點且 ![]() +
+ ![]() +2
+2 ![]() =
= ![]() ,現將3000粒黃豆隨機拋在△ABC內,則落在△PBC內的黃豆數大約是 .
,現將3000粒黃豆隨機拋在△ABC內,則落在△PBC內的黃豆數大約是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四棱錐P﹣ABCD中,PD⊥平面ABCD,BC⊥CD,PD=1,AB= ![]() ,BC=CD=
,BC=CD= ![]() ,AD=1.
,AD=1. 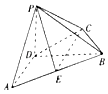
(1)求異面直線AB、PC所成角的余弦值;
(2)點E是線段AB的中點,求二面角E﹣PC﹣D的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,D、E分別是△ABC的三等分點,設 ![]() =
= ![]() ,
, ![]() =
= ![]() ,∠BAC=
,∠BAC= ![]() .
.
(1)用 ![]() ,
, ![]() 分別表示
分別表示 ![]() ,
, ![]() ;
;
(2)若 ![]()
![]() =15,|
=15,| ![]() |=3
|=3 ![]() ,求△ABC的面積.
,求△ABC的面積. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,為測一樹的高度,在地面上選取A、B兩點,從A、B兩點分別測得樹尖的仰角為30°、45°,且A、B兩點之間的距離為60m,則樹的高度為( ) 
A.(30+30 ![]() ) m
) m
B.(30+15 ![]() ) m??
) m??
C.(15+30 ![]() ) m
) m
D.(15+15 ![]() ) m
) m
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中真命題為( )
A.過點P(x0 , y0)的直線都可表示為y﹣y0=k(x﹣x0)
B.過兩點(x1 , y1),(x2 , y2)的直線都可表示為(x﹣x1)(y2﹣y1)=(y﹣y1)(x2﹣x1)
C.過點(0,b)的所有直線都可表示為y=kx+b
D.不過原點的所有直線都可表示為 ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com