
【題目】已知函數(shù)![]() .
.
(1)當函數(shù)![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,求函數(shù)
,求函數(shù)![]() 的解析式;
的解析式;
(2)在(1)的條件下,若![]() 是函數(shù)
是函數(shù)![]() 的零點,且
的零點,且![]() ,求
,求![]() 的值;
的值;
(3)當![]() 時,函數(shù)
時,函數(shù)![]() 有兩個零點
有兩個零點![]() ,且
,且![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】
試題分析:(1)先求出![]() 的導函數(shù),再根據(jù)
的導函數(shù),再根據(jù)![]() 且
且![]() 可以求得
可以求得![]() 的值進而得函數(shù)
的值進而得函數(shù)![]() 的解析式;(2)先根據(jù)導數(shù)研究函數(shù)
的解析式;(2)先根據(jù)導數(shù)研究函數(shù)![]() 的單調(diào)性,再根據(jù)零點定理判定出零點
的單調(diào)性,再根據(jù)零點定理判定出零點![]() 所在區(qū)間即可求得
所在區(qū)間即可求得![]() 的值;(3)根據(jù)
的值;(3)根據(jù)![]() 做差先將
做差先將![]() 表示成關于
表示成關于![]() 的函數(shù)
的函數(shù)![]() ,然后證明
,然后證明![]() 即可.
即可.
試題解析: (1)![]() ,所以
,所以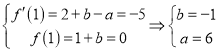 ,
,
∴函數(shù)![]() 的解析式為
的解析式為![]() ;
;
(2)![]() ,
,
因為函數(shù)![]() 的定義域為
的定義域為![]() ,
,
令![]() ,
,
當![]() 時,
時,![]() ,
,![]() 單調(diào)遞減,
單調(diào)遞減,
當![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 單調(diào)遞增,
單調(diào)遞增,
且函數(shù)![]() 的定義域為
的定義域為![]() ,
,
令![]() ,
,
且![]() 時,
時,![]() 單調(diào)遞減,
單調(diào)遞減,
當![]() 時,
時,![]() ,
,![]() 單調(diào)遞增,
單調(diào)遞增,
且函數(shù)![]() 至少有1個零點,而
至少有1個零點,而![]() ,不符合要求,
,不符合要求,
![]() ,
,
∴![]() ,故
,故![]() .
.
(3)當![]() 時,函數(shù)
時,函數(shù)![]() ,
,
![]() ,兩式相減可得
,兩式相減可得
![]() .
.
![]() ,因為
,因為![]() ,
,
所以![]()
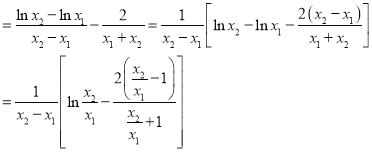
設![]() ,
,
∴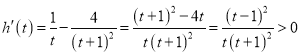 ,
,
所以![]() 在
在![]() 上為增函數(shù),且
上為增函數(shù),且![]() ,
,
∴![]() ,又
,又![]() ,所以
,所以![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】有一塊半徑為![]() 的正常數(shù))的半圓形空地,開發(fā)商計劃征地建一個矩形的游泳池
的正常數(shù))的半圓形空地,開發(fā)商計劃征地建一個矩形的游泳池![]() 和其附屬設施,附屬設施占地形狀是等腰
和其附屬設施,附屬設施占地形狀是等腰![]() ,其中
,其中![]() 為圓心,
為圓心, ![]() 在圓的直徑上,
在圓的直徑上, ![]() 在半圓周上,如圖.
在半圓周上,如圖.
(1)設![]() ,征地面積為
,征地面積為![]() ,求
,求![]() 的表達式,并寫出定義域;
的表達式,并寫出定義域;
(2)當![]() 滿足
滿足![]() 取得最大值時,開發(fā)效果最佳,求出開發(fā)效果最佳的角
取得最大值時,開發(fā)效果最佳,求出開發(fā)效果最佳的角![]() 的值,
的值,
求出![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】中央電視臺電視公開課《開講了》需要現(xiàn)場觀眾,先邀請甲、乙、丙、丁四所大學的40名學生參加,各大學邀請的學生如下表所示:
大學 | 甲 | 乙 | 丙 | 丁 |
人數(shù) | 8 | 12 | 8 | 12 |
從這40名學生中按分層抽樣的方式抽取10名學生在第一排發(fā)言席就座.
(1)求各大學抽取的人數(shù);
(2)從(1)中抽取的乙大學和丁大學的學生中隨機選出2名學生發(fā)言,求這2名學生來自同一所大學的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA![]() =4,點D是AB的中點
=4,點D是AB的中點

(1)求證:AC![]() BC
BC![]() ;
;
(2)求證:AC![]() //平面CDB
//平面CDB![]() ;
;
(3)求二面角B-DC-B1的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]()
![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
(1)若函數(shù)![]() 有實數(shù)零點,求滿足條件的實數(shù)
有實數(shù)零點,求滿足條件的實數(shù)![]() 的集合
的集合![]() ;
;
(2)若對于任意的![]() 時,不等式
時,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() .
.
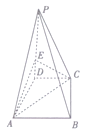
(1)在![]() 上確定一點
上確定一點![]() ,使得
,使得![]() 平面
平面![]() ,并求
,并求![]() 的值;
的值;
(2)在(1)條件下,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】函數(shù)![]() 的一段圖象如圖所示.
的一段圖象如圖所示.

(1)求函數(shù)![]() 的解析式;
的解析式;
(2)將函數(shù)![]() 的圖象向右平移
的圖象向右平移![]() 個單位,得到
個單位,得到![]() 的圖象,求直線
的圖象,求直線![]() 與
與
函數(shù)![]() 的圖象在
的圖象在![]() 內(nèi)所有交點的坐標.
內(nèi)所有交點的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知直線l:![]() 與圓O:
與圓O:![]() 相交于A,B兩個不同的點,且A
相交于A,B兩個不同的點,且A![]() ,B
,B![]() .
.
(1)當![]() 面積最大時,求m的取值,并求出
面積最大時,求m的取值,并求出![]() 的長度.
的長度.
(2)判斷![]() 是否為定值;若是,求出定值的大小;若不是,說明理由.
是否為定值;若是,求出定值的大小;若不是,說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com