
【題目】某超市計劃銷售某種食品,現邀請甲、乙兩個商家進場試銷10天.兩個商家向超市提供的日返利方案如下:甲商家每天固定返利60元,且每賣出一件食品商家再返利3元;乙商家無固定返利,賣出不超出30件(含30件)的食品,每件食品商家返利5元,超出30件的部分每件返利10元. 經統計,試銷這10天兩個商家每天的銷量如圖所示的莖葉圖(莖為十位數字,葉為個位數字):
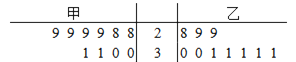
(1)現從甲商家試銷的10天中隨機抽取兩天,求這兩天的銷售量都小于30件的概率;
(2)根據試銷10天的數據,將頻率視作概率,用樣本估計總體,回答以下問題:
①記商家乙的日返利額為X(單位:元),求X的分布列和數學期望;
②超市擬在甲、乙兩個商家中選擇一家長期銷售,如果僅從日返利額的數學期望考慮,請利用所學的統計學知識為超市作出選擇,并說明理由.
【答案】(1)![]() ;(2)①分布列見解析,153;②由①得乙商家的日平均返利額為153元>148.2元,所以推薦該超市選擇乙商家長期銷售.
;(2)①分布列見解析,153;②由①得乙商家的日平均返利額為153元>148.2元,所以推薦該超市選擇乙商家長期銷售.
【解析】
(1)記“抽取的兩條銷售量都下于30件”為事件![]() ,利用排列組合即可求得答案;
,利用排列組合即可求得答案;
(2)①設乙商家的日銷售量為![]() ,推導出
,推導出![]() 的所有可能取值為:140,145,150,160,分別求出相應的概率,由此能求出
的所有可能取值為:140,145,150,160,分別求出相應的概率,由此能求出![]() 的分布列和
的分布列和![]() ;
;
②依題意,求出甲商家的日平均銷售量,從而求出甲商家的日平均返利額,再求出乙商家的日平均返利額,從而推薦該超市選擇乙商家長期銷售。
(1)記“抽取的兩天銷售量都小于30件”為事件A,則![]() .
.
(2)①設乙商家的日銷售量為![]() 件,則當
件,則當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .所以
.所以![]() 的所有可能取值為:140,145,150,160.
的所有可能取值為:140,145,150,160.
所以X的分布列為
| 140 | 145 | 150 | 160 |
|
|
|
|
|
所以![]() ;
;
②依題意,甲商家的日平均銷售量為:28×0.2+29×0.4+30×0.2+31×0.2=29.4.所以甲商家的日平均返利額為:60+29.4×3=148.2元.
由①得乙商家的日平均返利額為153元>148.2元,所以推薦該超市選擇乙商家長期銷售.


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸且取相同的單位長度建立極坐標系,曲線C的極坐標方程為
軸的非負半軸為極軸且取相同的單位長度建立極坐標系,曲線C的極坐標方程為![]() .
.
(1)求直線![]() 和曲線C的直角坐標方程;
和曲線C的直角坐標方程;
(2)若點P為曲線C上任一點,求點P到直線![]() 的距離的最大值,并求此時點P的坐標.
的距離的最大值,并求此時點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高校為了解即將畢業的男大學生的身體狀況檢測了960名男大學生的體重(單位:![]() ),所得數據都在區間
),所得數據都在區間![]() 中,其頻率分布直方圖如圖所示.圖中從左到右的前3個小組的頻率之比為
中,其頻率分布直方圖如圖所示.圖中從左到右的前3個小組的頻率之比為![]() .
.
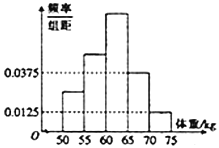
(1)求這960名男大學生中,體重小于![]() 的男大學生的人數;
的男大學生的人數;
(2)從體重在![]() 范圍的男大學生中用分層抽樣的方法選取6名,再從這6名男大學生中隨機選取2名,記“至少有一名男大學生體重大于
范圍的男大學生中用分層抽樣的方法選取6名,再從這6名男大學生中隨機選取2名,記“至少有一名男大學生體重大于![]() ”為事件
”為事件![]() ,求事件
,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】未來創造業對零件的精度要求越來越高.![]() 打印通常是采用數字技術材料打印機來實現的,常在模具制造、工業設計等領域被用于制造模型,后逐漸用于一些產品的直接制造,已經有使用這種技術打印而成的零部件.該技術應用十分廣泛,可以預計在未來會有發展空間.某制造企業向
打印通常是采用數字技術材料打印機來實現的,常在模具制造、工業設計等領域被用于制造模型,后逐漸用于一些產品的直接制造,已經有使用這種技術打印而成的零部件.該技術應用十分廣泛,可以預計在未來會有發展空間.某制造企業向![]() 高校
高校![]() 打印實驗團隊租用一臺
打印實驗團隊租用一臺![]() 打印設備,用于打印一批對內徑有較高精度要求的零件.該團隊在實驗室打印出了一批這樣的零件,從中隨機抽取
打印設備,用于打印一批對內徑有較高精度要求的零件.該團隊在實驗室打印出了一批這樣的零件,從中隨機抽取![]() 個零件,度量其內徑的莖葉圖如圖(單位:
個零件,度量其內徑的莖葉圖如圖(單位:![]() ).
).

(1)計算平均值![]() 與標準差
與標準差![]() ;
;
(2)假設這臺![]() 打印設備打印出品的零件內徑
打印設備打印出品的零件內徑![]() 服從正態分布
服從正態分布![]() ,該團隊到工廠安裝調試后,試打了
,該團隊到工廠安裝調試后,試打了![]() 個零件,度量其內徑分別為(單位:
個零件,度量其內徑分別為(單位:![]() ):
):![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,試問此打印設備是否需要進一步調試?為什么?
,試問此打印設備是否需要進一步調試?為什么?
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】依法納稅是每個公民應盡的義務,個人取得的所得應依照《中華人民共和國個人所得稅法》向國家繳納個人所得稅(簡稱個稅).2019年1月1日起,個稅稅額根據應納稅所得額、稅率和速算扣除數確定,計算公式為:個稅稅額=應納稅所得額×稅率-速算扣除數.應納稅所得額的計算公式為:應納稅所得額=綜合所得收入額-基本減除費用-專項扣除-專項附加扣除-依法確定的其它扣除.
其中,“基本減除費用”(免征額)為每年60000元.稅率與速算扣除數見下表:
級數 | 全年應納稅所得額所在區間 | 稅率( | 速算扣除數 |
1 |
| 3 | 0 |
2 |
| 10 | 2520 |
3 |
| 20 | 16920 |
… | … | … | … |
(1)設全年應納稅所得額為![]() 元,應繳納個稅稅額為
元,應繳納個稅稅額為![]() 元,求
元,求![]() ;
;
(2)小王全年綜合所得收入額為189600元,假定繳納的基本養老金、基本醫療保險費、失業保險等社會保險費和住房公積金占綜合所得收入額的比例分別是![]() ,
,![]() ,
,![]() ,
,![]() ,專項附加扣除是52800元,依法確定其它扣除是4560元,那么他全年應繳納多少綜合所得個稅?
,專項附加扣除是52800元,依法確定其它扣除是4560元,那么他全年應繳納多少綜合所得個稅?
(3)設小王年綜合所得收入額為![]() 元,應繳納綜合所得個稅稅額為
元,應繳納綜合所得個稅稅額為![]() 元,求
元,求![]() 關于
關于![]() 的函數解析式;并計算小王全年綜合所得收入額由189600元增加到249600元,那么他全年繳納多少綜合所得個稅?
的函數解析式;并計算小王全年綜合所得收入額由189600元增加到249600元,那么他全年繳納多少綜合所得個稅?
注:“綜合所得”包括工資、薪金,勞務報酬,稿酬,特許權使用費;“專項扣除”包括居民個人按照國家規定的范圍和標準繳納的基本養老保險、基本醫療保險費、失業保險等社會保險費和住房公積金等;“專項附加扣除”包括子女教育、繼續教育、大病醫療、住房貸款利息或者住房租金、贍養老人等支出;“其他扣除”是指除上述基本減除費用、專項扣除、專項附加扣除之外,由國務院決定以扣除方式減少納稅的優惠政策規定的費用.
查看答案和解析>>
科目:高中數學 來源: 題型:
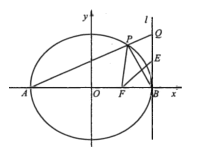
【題目】在平面直角坐標系xOy中,己知橢圓C:![]() 的左、右頂點為A,B,右焦點為F.過點A且斜率為k(
的左、右頂點為A,B,右焦點為F.過點A且斜率為k(![]() )的直線交橢圓C于另一點P.
)的直線交橢圓C于另一點P.
(1)求橢圓C的離心率;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)設直線l:![]() ,延長AP交直線l于點Q,線段BO的中點為E,求證:點B關于直線EF的對稱點在直線PF上。
,延長AP交直線l于點Q,線段BO的中點為E,求證:點B關于直線EF的對稱點在直線PF上。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com