
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸且取相同的單位長度建立極坐標系,曲線C的極坐標方程為
軸的非負半軸為極軸且取相同的單位長度建立極坐標系,曲線C的極坐標方程為![]() .
.
(1)求直線![]() 和曲線C的直角坐標方程;
和曲線C的直角坐標方程;
(2)若點P為曲線C上任一點,求點P到直線![]() 的距離的最大值,并求此時點P的坐標.
的距離的最大值,并求此時點P的坐標.
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 在統計學中,回歸分析是檢驗兩個分類變量是否有關系的一種統計方法
B. 線性回歸方程對應的直線![]() 至少經過其樣本數據點中的
至少經過其樣本數據點中的![]() ,
,![]() ,
,![]()
![]() 一個點
一個點
C. 在殘差圖中,殘差點分布的帶狀區域的寬度越狹窄,其模型擬合的精度越高
D. 在回歸分析中,相關指數![]() 為
為![]() 的模型比相關指數
的模型比相關指數![]() 為
為![]() 的模型擬合的效果差
的模型擬合的效果差
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】禽流感一直在威脅我們的生活,某疾病控制中心為了研究禽流感病毒繁殖個數![]() (個)隨時間
(個)隨時間![]() (天)變化的規律,收集數據如下:
(天)變化的規律,收集數據如下:
天數 | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖個數 | 6 | 12 | 25 | 49 | 95 | 190 |
作出散點圖可看出樣本點分布在一條指數型函數![]() 的周圍.
的周圍.
保留小數點后兩位數的參考數據:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]()
(1)求出![]() 關于
關于![]() 的回歸方程(保留小數點后兩位數字);
的回歸方程(保留小數點后兩位數字);
(2)已知![]() ,估算第四天的殘差.
,估算第四天的殘差.
參考公式: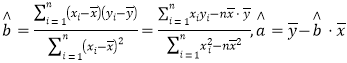
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四邊形![]() 為直角梯形,
為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 中點,
中點,![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,沿
,沿![]() 將四邊形
將四邊形![]() 折起,連接
折起,連接![]() .
.
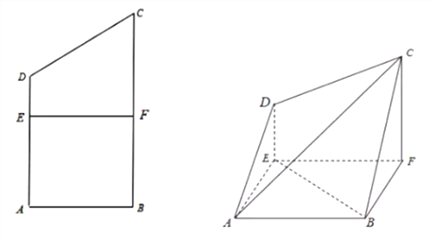
(1)求證:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() .
.
(I)求二面角![]() 的平面角的大小;
的平面角的大小;
(II)線段![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,如果存在常數p,使得對任意正整數n,總有
,如果存在常數p,使得對任意正整數n,總有![]() 成立,那么我們稱數列
成立,那么我們稱數列![]() 為“p-擺動數列”.
為“p-擺動數列”.
(Ⅰ)設![]() ,
,![]() ,
,![]() ,判斷
,判斷![]() 、
、![]() 是否為“p-擺動數列”,并說明理由;
是否為“p-擺動數列”,并說明理由;
(Ⅱ)已知“p-擺動數列”![]() 滿足
滿足![]() ,
,![]() ,求常數p的值;
,求常數p的值;
(Ⅲ)設![]() ,且數列
,且數列![]() 的前n項和為
的前n項和為![]() ,求證:數列
,求證:數列![]() 是“p-擺動數列”,并求出常數p的取值范圍.
是“p-擺動數列”,并求出常數p的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 、
、![]() 、
、![]() ,且
,且![]() 都有
都有![]() ,滿足
,滿足![]() 的實數
的實數![]() 有且只有
有且只有![]() 個,給出下述四個結論:
個,給出下述四個結論:
①滿足題目條件的實數![]() 有且只有
有且只有![]() 個;②滿足題目條件的實數
個;②滿足題目條件的實數![]() 有且只有
有且只有![]() 個;
個;
③![]() 在
在![]() 上單調遞增;④
上單調遞增;④![]() 的取值范圍是
的取值范圍是![]() .
.
其中所有正確結論的編號是( )
A.①④B.②③C.①②③D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市計劃銷售某種食品,現邀請甲、乙兩個商家進場試銷10天.兩個商家向超市提供的日返利方案如下:甲商家每天固定返利60元,且每賣出一件食品商家再返利3元;乙商家無固定返利,賣出不超出30件(含30件)的食品,每件食品商家返利5元,超出30件的部分每件返利10元. 經統計,試銷這10天兩個商家每天的銷量如圖所示的莖葉圖(莖為十位數字,葉為個位數字):
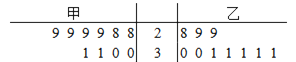
(1)現從甲商家試銷的10天中隨機抽取兩天,求這兩天的銷售量都小于30件的概率;
(2)根據試銷10天的數據,將頻率視作概率,用樣本估計總體,回答以下問題:
①記商家乙的日返利額為X(單位:元),求X的分布列和數學期望;
②超市擬在甲、乙兩個商家中選擇一家長期銷售,如果僅從日返利額的數學期望考慮,請利用所學的統計學知識為超市作出選擇,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com