解:(1)∵

,

,
又

,
而y=sinx在

上遞減,
∴
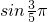
>

,即
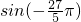
>
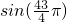
.
(2)∵tan2007°=tan207°,tan2008°=tan208°,
又180°<207°<208°<270°,
而y=tanx在(180°,270°)上遞增,
∴tan207°<tan208°,即tan2007°<tan2008°.
分析:(1)先利用誘導公式化簡,
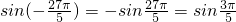
,sin

,利用正弦函數y=sinx在區間

上的單調性判斷.
(2)利用誘導公式化簡可得,tan2007°=tan(1800
0+207
0)=tan207°,tan2008°=tan208°,結合正切函數y=tanx在(180
0,270
0)上的單調性可判斷tan207°與tan208°的大小,從而判斷原式的大小.
點評:本題主要考查了正弦函數y=sinx,y=tanx在相應區間上的單調性的應用,利用單調性判斷函數值的大小的前提是先用誘導公式把函數式化簡到同一個單調區間,然后利用函數在單調區間上的單調性進行判斷.

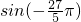 和
和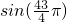 ;
; ,
, ,
, ,
, 上遞減,
上遞減,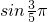 >
> ,即
,即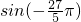 >
>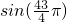 .
.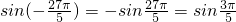 ,sin
,sin ,利用正弦函數y=sinx在區間
,利用正弦函數y=sinx在區間 上的單調性判斷.
上的單調性判斷.
