
【題目】已知函數![]() 是定義域為
是定義域為![]() 的周期為3的奇函數,且當
的周期為3的奇函數,且當![]() 時,
時,![]() ,則方程
,則方程![]() 在區間
在區間![]() 上的解得個數是( )
上的解得個數是( )
A. ![]() B. 6 C. 7 D. 9
B. 6 C. 7 D. 9
【答案】D
【解析】分析:要求方程f(x)=0在區間[0,6]上的解的個數,根據函數f(x)是定義域為R的周期為3的奇函數,且當x∈(0,1.5)時f(x)=ln(x2﹣x+1),我們不難得到一個周期函數零點的個數,根據周期性進行分析不難得到結論.
詳解:∵當x∈(0,1.5)時f(x)=ln(x2﹣x+1),
令f(x)=0,則x2﹣x+1=1,解得x=1
又∵函數f(x)是定義域為R的奇函數,
∴在區間∈[﹣1.5,1.5]上,
f(﹣1)=f(1)=0,
f(0)=0
f(1.5)=f(﹣1.5+3)=f(﹣1.5)=﹣f(﹣1.5)
∴f(﹣1)=f(1)=f(0)=f(1.5)=f(﹣1.5)=0
又∵函數f(x)是周期為3的周期函數
則方程f(x)=0在區間[0,6]上的解有0,1,1.5,2,3,4,4.5,5,6
共9個
故選:D.


科目:高中數學 來源: 題型:
【題目】己知函數![]() .(
.(![]() 是常數,且(
是常數,且(![]() )
)
(Ⅰ)求函數![]() 的單調區間;
的單調區間;
(Ⅱ)當![]() 在
在![]() 處取得極值時,若關于
處取得極值時,若關于![]() 的方程
的方程![]() 在
在![]() 上恰有兩個不相等的實數根,求實數
上恰有兩個不相等的實數根,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)求證:當![]() 時
時![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=|x﹣a|+|x![]() |(a>0).
|(a>0).
(1)若不等式f(x)﹣| x![]() |≥4x的解集為{x|x≤1},求實數a的值;
|≥4x的解集為{x|x≤1},求實數a的值;
(2)證明:f(x)![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一項研究中,為盡快攻克某一課題,某生物研究所分別設立了甲、乙兩個研究小組同時進行對比試驗,現隨機在這兩個小組各抽取40個數據作為樣本,并規定試驗數據落在[495,510)之內的數據作為理想數據,否則為不理想數據.試驗情況如表所示

(1)由以上統計數據完成下面2×2列聯表;
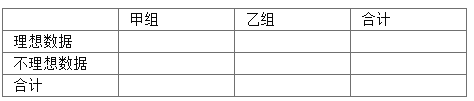
(2)判斷是否有90%的把握認為抽取的數據為理想數據與對兩個研究小組的選擇有關;說明你的理由;(下面的臨界值表供參考)

(參考公式: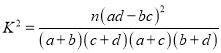 其中n=a+b+c+d)
其中n=a+b+c+d)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓具有如下性質:若![]() 、
、![]() 是橢圓
是橢圓![]() 上關于原點對稱的兩個點,點
上關于原點對稱的兩個點,點![]() 是橢圓上的任意一點,當直線
是橢圓上的任意一點,當直線![]() 、
、![]() 的斜率都存在,并記為
的斜率都存在,并記為![]() 、
、![]() 時,則
時,則![]() 與
與![]() 之積是與點
之積是與點![]() 位置無關的定值.試寫出雙曲線
位置無關的定值.試寫出雙曲線![]() 具有的類似的性質,并加以證明.
具有的類似的性質,并加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 汽車站每天上午
汽車站每天上午![]() ,
,![]() 之間都恰有一輛長途汽車經過,但是長途車到站的時間是隨機的,且每輛車的到站時間是相互獨立的,汽車到站后即停即走,據統計汽車到站規律為:
之間都恰有一輛長途汽車經過,但是長途車到站的時間是隨機的,且每輛車的到站時間是相互獨立的,汽車到站后即停即走,據統計汽車到站規律為:

現有一位旅客在![]() 到達
到達![]() 汽車站,問:
汽車站,問:
(1)該旅客候車時間不超過20分鐘的概率;
(2)記該旅客的候車時間為![]() ,求
,求![]() 的概率分布列及數學期望.
的概率分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若數列![]() 滿足:對于任意
滿足:對于任意![]() 均為數列
均為數列![]() 中的項,則稱數列
中的項,則稱數列![]() 為“
為“![]() 數列”.
數列”.
(1)若數列![]() 的前
的前![]() 項和
項和![]() ,求證:數列
,求證:數列![]() 為“
為“![]() 數列”;
數列”;
(2)若公差為![]() 的等差數列
的等差數列![]() 為“
為“![]() 數列”,求
數列”,求![]() 的取值范圍;
的取值范圍;
(3)若數列![]() 為“
為“![]() 數列”,
數列”,![]() ,且對于任意
,且對于任意![]() ,均有
,均有![]() ,求數列
,求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點 .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過橢圓![]() 的左焦點的直線
的左焦點的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,直線
兩點,直線![]() 過坐標原點且與直線
過坐標原點且與直線![]() 的斜率互為相反數.若直線
的斜率互為相反數.若直線![]() 與橢圓交于
與橢圓交于![]() 兩點且均不與點
兩點且均不與點![]() 重合,設直線
重合,設直線![]() 與
與![]() 軸所成的銳角為
軸所成的銳角為![]() ,直線
,直線![]() 與
與![]() 軸所成的銳角為
軸所成的銳角為![]() ,判斷
,判斷![]() 與
與![]() 的大小關系并加以證明.
的大小關系并加以證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com