
(Ⅰ)求f(x)的解析式;
(Ⅱ)是否存在區間[a,b],使得函數g(x)的定義域和值域均為[a,b],且解析式與f(x)的解析式相同?若存在,求出這樣的一個區間[a,b];若不存在,請說明理由.
答案:解:(Ⅰ)由已知有f(x)是奇函數,所以b=d=0.
又在x=3的切線方程為8x-y-18=0,
所以切點為(3,6),且f′(x)|x=3=8.
而f′(x)=3ax2+c,所以有![]()
即得a=![]() ,c=-1.故f(x)=
,c=-1.故f(x)=![]() x3-x.
x3-x.
(Ⅱ)解方程組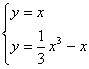 ,得x1=0,x2=
,得x1=0,x2=![]() ,x3=
,x3=![]() ,且f(
,且f(![]() )=
)=![]() ,f(
,f(![]() )=
)=![]() .
.
又f′(x)=x2-1,令f′(x)=x2-1=0,得x=±1.
所以f′(x)在(-![]() ,-1)和(1,+∞)上都有f′(x)>0,f′(x)在(-1,1)上f′(x)<0,故f(x)在(-∞,-1)和(1,+∞)上都為增函數,在(-1,1)上為減函數.
,-1)和(1,+∞)上都有f′(x)>0,f′(x)在(-1,1)上f′(x)<0,故f(x)在(-∞,-1)和(1,+∞)上都為增函數,在(-1,1)上為減函數.
所以f(x)在x=1處有極小值![]() ,在x=-1處有極大值
,在x=-1處有極大值![]() .
.
而極小值f(1)=![]() >
>![]() =f(
=f(![]() ),
),
極大值f(-1)=![]() <
<![]() =f(
=f(![]() ),
),
所以f(x)max=![]() ,f(x)min=
,f(x)min=![]() .
.
所以f(x)在區間[![]() ,
,![]() ]上的值域為[
]上的值域為[![]() ,
,![]() ].
].
綜合以上得:存在區間[a,b]=[![]() ,
,![]() ]符合要求.
]符合要求.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案 各地期末復習特訓卷系列答案
各地期末復習特訓卷系列答案科目:高中數學 來源: 題型:
| 1 | 2x+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| a(x-1) | x2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2x-1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com