
 如圖,在Rt△ABC中,∠ACB=90°,∠B=30°,D,E分)別為AB,CD的中點,AE的延長線交CB于F.現將△ACD沿CD折起,折成二面角A-CD-B,連接AF.
如圖,在Rt△ABC中,∠ACB=90°,∠B=30°,D,E分)別為AB,CD的中點,AE的延長線交CB于F.現將△ACD沿CD折起,折成二面角A-CD-B,連接AF.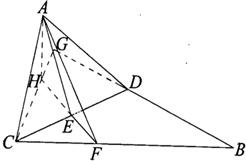 解:
解:
(I)證明:在Rt△ABC中,D為AB的中點,得AD=CD=DB,
又∠B=30°,得△ACD是正三角形,
又E是CD的中點,得AF⊥CD.
折起后,AE⊥CD,EF⊥CD,
又AE∩EF=E,AE?平面AED,EF?平面AEF,
故CD⊥平面AEF,
又CD?平面CDB,
故平面AEF⊥平面CBD.
(II)過點A作AH⊥EF,垂足H落在FE的延長線,
因為CD⊥平面AEF,所以CD⊥AH,
所以AH⊥平面CBD.
連接CH并延長交BD的延長線于G,
由已知AC⊥BD,得CH⊥BD,可得BD垂直于面AHC,從而得到BD垂直于線CG
可得∠CGB=90°,
因此△CEH∽△CGD,
則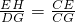 ,
,
設AC=a,易得
∠GDC=60°,DG= ,
,
代入上式得EH=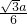 ,
,
又EA=
故cos∠HEA= .
.
又∵AE⊥CD,EF⊥CD,
∴∠AEF即為所求二面角的平面角,
故二面角A-CD-B大小的余弦值為- .
.


科目:高中數學 來源: 題型:
 如圖,在Rt△ABC中,∠ACB=90°,以AC為直徑的⊙O與AB邊交于點D,過點D作⊙O的切線,交BC于點E.
如圖,在Rt△ABC中,∠ACB=90°,以AC為直徑的⊙O與AB邊交于點D,過點D作⊙O的切線,交BC于點E.| 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于點P.
如圖,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于點P.查看答案和解析>>
科目:高中數學 來源: 題型:
 8.如圖,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如圖,在Rt△ABC中,∠CAB=90°,AB=2,AC=
| ||
| 2 |
| DM |
| DN |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在Rt△ABC中,AC=1,BC=x,D是斜邊AB的中點,將△BCD沿直線CD翻折,若在翻折過程中存在某個位置,使得CB⊥AD,則x的取值范圍是( )
如圖,在Rt△ABC中,AC=1,BC=x,D是斜邊AB的中點,將△BCD沿直線CD翻折,若在翻折過程中存在某個位置,使得CB⊥AD,則x的取值范圍是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com