
【題目】設數組![]() ,
,![]() ,
,![]()
![]() ,數
,數![]() 稱為數組
稱為數組![]() 的元素.對于數組
的元素.對于數組![]() ,規定:
,規定:
①數組![]() 中所有元素的和為
中所有元素的和為![]() ;
;
②變換![]() ,
,![]() 將數組
將數組![]() 變換成數組
變換成數組![]() ,其中
,其中![]() 表示不超過
表示不超過![]() 的最大整數;
的最大整數;
③若數組![]() ,則當且僅當
,則當且僅當![]()
![]() 時,
時,![]() .
.
如果對數組![]() 中任意
中任意![]() 個元素,存在一種分法,可將其分為兩組,每組
個元素,存在一種分法,可將其分為兩組,每組![]() 個元素,使得兩組所有元素的和相等,則稱數組
個元素,使得兩組所有元素的和相等,則稱數組![]() 具有性質
具有性質![]() .
.
(Ⅰ)已知數組![]() ,
,![]() ,計算
,計算![]() ,
,![]() ,并寫出數組
,并寫出數組![]() 是否具有性質
是否具有性質![]() ;
;
(Ⅱ)已知數組![]() 具有性質
具有性質![]() ,證明:
,證明:![]() 也具有性質
也具有性質![]() ;
;
(Ⅲ)證明:數組![]() 具有性質
具有性質![]() 的充要條件是
的充要條件是![]() .
.
【答案】(Ⅰ)數組![]() 是具有性質
是具有性質![]() ,數組
,數組![]() 不具有性質
不具有性質![]() .(Ⅱ)證明見解析(Ⅲ)證明見解析
.(Ⅱ)證明見解析(Ⅲ)證明見解析
【解析】
(Ⅰ)根據題意,即可容易得![]() ,則可判斷;
,則可判斷;
(Ⅱ)對![]() 都為奇數和都為偶數,結合性質
都為奇數和都為偶數,結合性質![]() 的定義,即可證明;
的定義,即可證明;
(Ⅲ)從充分性和必要性上,結合(Ⅱ)中所求,即可證明.
(Ⅰ)![]() ,
,![]() ;
;
數組![]() 是具有性質
是具有性質![]() ,數組
,數組![]() 不具有性質
不具有性質![]() .
.
(Ⅱ)證明:當元素![]() 均為奇數時,
均為奇數時,
因為![]() ,
,![]() ,所以
,所以![]() .
.
對![]() 中任意
中任意![]() 個元素,不妨設為
個元素,不妨設為![]() .
.
因為數組![]() 具有性質
具有性質![]() ,所以對于
,所以對于![]() ,
,
存在一種分法:將其分為兩組,每組![]() 個素,使得各組內所有元素之和相等.
個素,使得各組內所有元素之和相等.
如果用![]() 替換上述分法中的
替換上述分法中的![]() (
(![]() ),
),
就可以得到對于![]() 的一種分法:
的一種分法:
將其分為兩組,每組![]() 個元素,顯然各組內所有元素之和相等.
個元素,顯然各組內所有元素之和相等.
所以此時![]() 也具有性質
也具有性質![]() .
.
當元素![]() 均為偶數時,
均為偶數時,
因為![]() ,
,![]() ,所以
,所以![]() .
.
對![]() 中任意
中任意![]() 個元素,不妨設為
個元素,不妨設為![]() .
.
因為數組![]() 具有性質
具有性質![]() ,所以對于
,所以對于![]() ,
,
存在一種分法:將其分為兩組,每組![]() 個元素,使得各組內所有元素之和相等.
個元素,使得各組內所有元素之和相等.
如果用![]() 替換上述分法中的
替換上述分法中的![]() (
(![]() ),
),
就可以得到對于![]() 的一種分法:
的一種分法:
將其分為兩組,每組![]() 個元素,顯然各組內所有元素之和相等.
個元素,顯然各組內所有元素之和相等.
所以此時![]() 也具有性質
也具有性質![]() .
.
綜上所述,由數組![]() 具有性質
具有性質![]() 可得
可得![]() 也具有性質
也具有性質![]() .
.
(Ⅲ)證明:(1)充分性:顯然成立.
(2)必要性:
因為數組![]() 具有性質
具有性質![]() ,所以對于數組
,所以對于數組![]() 中任意
中任意![]() 個元素,存在一種分法:
個元素,存在一種分法:
將![]() 個元素平均分成2組,并且各組內所有元素之和等于同一個正整數,
個元素平均分成2組,并且各組內所有元素之和等于同一個正整數,
所以![]() 均為偶數,從而元素
均為偶數,從而元素![]() 的奇偶性相同.
的奇偶性相同.
由(Ⅱ)可知,如果數組![]() 具有性質
具有性質![]() ,
,
那么![]() 仍具有性質
仍具有性質![]() .
.
又因為,當![]() 為奇數時,
為奇數時,
![]() ,當且僅當
,當且僅當![]() 時等號成立,
時等號成立,
當![]() 為偶數時,
為偶數時,
![]() ,
,
由此得到![]() 的充要條件是
的充要條件是![]() .
.
易知![]() ,
,
當且僅當![]() 時等號成立.
時等號成立.
即![]() ,當且僅當
,當且僅當![]() 時等號成立.
時等號成立.
令![]() ,
,![]() ,
,![]() .
.
假設對于任意的![]() ,有
,有![]() ,則
,則![]() ,
,
又![]() ,
,![]() ,得
,得![]() ,即
,即![]() .
.
得![]() ,…,
,…,
![]() ,
,
所以![]() ,且
,且![]() 單調遞減.
單調遞減.
又因為![]() ,矛盾.
,矛盾.
所以存在![]() ,有
,有![]() .
.
又由結論1,得此時![]() .
.
上述過程倒推回去,
因為數組![]() 均具有性質
均具有性質![]() ,即數組
,即數組![]() 中元素
中元素![]()
的奇偶性相同,可得數組![]() 中的所有元素都相同,
中的所有元素都相同,
所以,數組![]() 中的元素均相同,即
中的元素均相同,即![]() .
.


 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 與
與![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 與
與![]() 的交于
的交于![]() 點,
點,![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點,求
兩點,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年安慶市在大力推進城市環境、人文精神建設的過程中,居民生活垃圾分類逐漸形成意識.有關部門為宣傳垃圾分類知識,面向該市市民進行了一次“垃圾分類知識"的網絡問卷調查,每位市民僅有一次參與機會,通過抽樣,得到參與問卷調查中的1000人的得分數據,其頻率分布直方圖如圖:
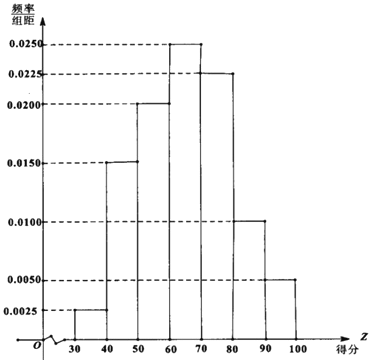
(1)由頻率分布直方圖可以認為,此次問卷調查的得分Z服從正態分布![]() ,
,![]() 近似為這1000人得分的平均值(同一組數據用該區間的中點值作代表),利用該正態分布,求P(
近似為這1000人得分的平均值(同一組數據用該區間的中點值作代表),利用該正態分布,求P(![]() );
);
(2)在(1)的條件下,有關部門為此次參加問卷調查的市民制定如下獎勵方案:
(i)得分不低于![]() 可獲贈2次隨機話費,得分低于
可獲贈2次隨機話費,得分低于![]() 則只有1次:
則只有1次:
(ii)每次贈送的隨機話費和對應概率如下:
贈送話費(單位:元) | 10 | 20 |
概率 |
|
|
現有一位市民要參加此次問卷調查,記X(單位:元)為該市民參加問卷調查獲贈的話費,求X的分布列.附:![]() ,若
,若![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】密云某商場舉辦春節優惠酬賓贈券活動,購買百元以上單件商品可以使用優惠劵一張,并且每天購物只能用一張優惠券.一名顧客得到三張優惠券,三張優惠券的具體優惠方式如下:
優惠券1:若標價超過50元,則付款時減免標價的10%;
優惠券2:若標價超過100元,則付款時減免20元;
優惠券3:若標價超過100元,則超過100元的部分減免18%.
如果顧客需要先用掉優惠券1,并且使用優惠券1比使用優惠券2、優惠券3減免的都多,那么你建議他購買的商品的標價可以是__________元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】秉承“綠水青山就是金山銀山”的發展理念,某市環保部門通過制定評分標準,先對本市的企業進行評估,評出四個等級,并根據等級給予相應的獎懲,如下表所示:
評估得分 |
|
|
|
|
評定等級 | 不合格 | 合格 | 良好 | 優秀 |
獎勵(萬元) |
|
|
|
|
環保部門對企業評估完成后,隨機抽取了![]() 家企業的評估得分(
家企業的評估得分(![]() 分)為樣本,得到如下頻率分布表:
分)為樣本,得到如下頻率分布表:
評估得分 |
|
|
|
|
|
|
頻率 |
|
|
|
|
|
|
其中![]() 、
、![]() 表示模糊不清的兩個數字,但知道樣本評估得分的平均數是
表示模糊不清的兩個數字,但知道樣本評估得分的平均數是![]() .
.
(1)現從樣本外的數百個企業評估得分中隨機抽取![]() 個,若以樣本中頻率為概率,求該家企業的獎勵不少于
個,若以樣本中頻率為概率,求該家企業的獎勵不少于![]() 萬元的概率;
萬元的概率;
(2)現從樣本“不合格”、“合格”、“良好”三個等級中,按分層抽樣的方法抽取![]() 家企業,再從這
家企業,再從這![]() 家企業隨機抽取
家企業隨機抽取![]() 家,求這兩家企業所獲獎勵之和不少于
家,求這兩家企業所獲獎勵之和不少于![]() 萬元的概率.
萬元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年末,武漢出現新型冠狀病毒肺炎(![]() )疫情,并快速席卷我國其他地區,傳播速度很快.因這種病毒是以前從未在人體中發現的冠狀病毒新毒株,所以目前沒有特異治療方法,防控難度很大.武漢市出現疫情最早,感染人員最多,防控壓力最大,武漢市從2月7日起舉全市之力入戶上門排查確診的新冠肺炎患者、疑似的新冠肺炎患者、無法明確排除新冠肺炎的發熱患者和與確診患者的密切接觸者等“四類”人員,強化網格化管理,不落一戶、不漏一人.在排查期間,一戶6口之家被確認為“與確診患者的密切接觸者”,這種情況下醫護人員要對其家庭成員隨機地逐一進行“核糖核酸”檢測,若出現陽性,則該家庭為“感染高危戶”.設該家庭每個成員檢測呈陽性的概率均為
)疫情,并快速席卷我國其他地區,傳播速度很快.因這種病毒是以前從未在人體中發現的冠狀病毒新毒株,所以目前沒有特異治療方法,防控難度很大.武漢市出現疫情最早,感染人員最多,防控壓力最大,武漢市從2月7日起舉全市之力入戶上門排查確診的新冠肺炎患者、疑似的新冠肺炎患者、無法明確排除新冠肺炎的發熱患者和與確診患者的密切接觸者等“四類”人員,強化網格化管理,不落一戶、不漏一人.在排查期間,一戶6口之家被確認為“與確診患者的密切接觸者”,這種情況下醫護人員要對其家庭成員隨機地逐一進行“核糖核酸”檢測,若出現陽性,則該家庭為“感染高危戶”.設該家庭每個成員檢測呈陽性的概率均為![]() (
(![]() )且相互獨立,該家庭至少檢測了5個人才能確定為“感染高危戶”的概率為
)且相互獨立,該家庭至少檢測了5個人才能確定為“感染高危戶”的概率為![]() ,當
,當![]() 時,
時,![]() 最大,則
最大,則![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某健身房為了解運動健身減肥的效果,調查了![]() 名肥胖者健身前(如直方圖(1)所示)后(如直方圖(2)所示)的體重(單位:
名肥胖者健身前(如直方圖(1)所示)后(如直方圖(2)所示)的體重(單位:![]() )變化情況:
)變化情況:
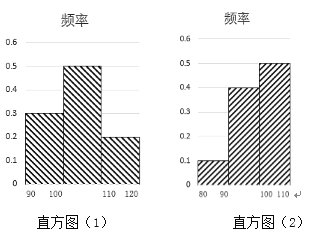
對比數據,關于這![]() 名肥胖者,下面結論正確的是( )
名肥胖者,下面結論正確的是( )
A.他們健身后,體重在區間![]() 內的人數較健身前增加了
內的人數較健身前增加了![]() 人
人
B.他們健身后,體重原在區間![]() 內的人員一定無變化
內的人員一定無變化
C.他們健身后,![]() 人的平均體重大約減少了
人的平均體重大約減少了![]()
D.他們健身后,原來體重在區間![]() 內的肥胖者體重都有減少
內的肥胖者體重都有減少
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com