已知直線
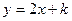
被拋物線
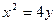
截得的
弦長
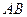
為20,
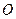
為坐標原點.
(1)求實數(shù)
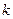
的值;
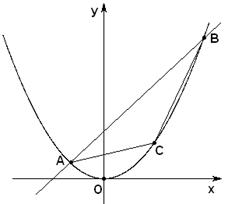
(2)問點
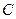
位于拋物線弧
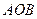
上何處時,△
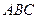
面積最大?
(1)
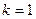
(2)

位于(4,4)點處
【解題思路】用“韋達定理”求弦長;考慮△
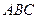
面積的最大值取得的條件
1)將
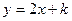
代入
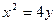
得

,
由△
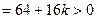
可知
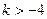
,
另一方面,弦長AB

,解得
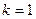
;
(2)當
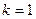
時,直線為
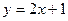
,要使得內(nèi)接△ABC面積最大,
則只須使得
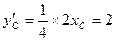
,
即

,即
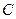
位于(4,4)點處.
【名師指引】用“韋達定理”不要忘記用判別式確定范圍
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:單選題
過拋物線y2=4x的頂點O作兩條互相垂直的直線分別交拋物線于A、B兩點,則線段AB的中點P(x,y)的軌跡方程是( )
A.y2="-2x-8 " B.y2=2x-8
C.y2="2x+8 " D.y2=-2x+8
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知拋物線的頂點在原點,對稱軸為
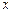
軸,拋物線上一點
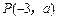
到焦點的距離為5,求拋物線的標準方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若點

與點
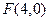
的距離比它到直線

的距離大

,則點

的軌跡
方程為__________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設拋物線
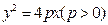
的準線與
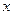
軸的交點為
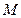
,過點
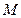
作直線
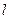
交拋物線于
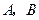
兩點.若直線
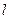
的斜率依次取
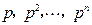
時,線段
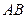
的垂直平分線與對稱軸的交點依次為

,當
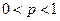
時,求
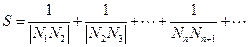
的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(1)頂點在原點,焦點在
y軸上,拋物線上點(3,
a)到焦點的距離是5;
(2)頂點在原點,焦點在
x軸上的拋物線截直線

所得的弦長為

。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
以x軸為準線,F(xiàn)(-1,-4)為焦點的拋物線方程
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
直線

過拋物線

的焦點,并且與

軸垂直,若

被拋物線截得的線段長為4,則

( )
| A. 4 | B. 2 | C. | D. |
查看答案和解析>>

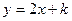 被拋物線
被拋物線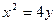 截得的
截得的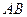 為20,
為20,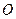 為坐標原點.
為坐標原點.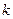 的值;
的值;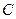 位于拋物線弧
位于拋物線弧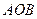 上何處時,△
上何處時,△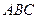 面積最大?
面積最大?
 閱讀快車系列答案
閱讀快車系列答案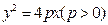 的準線與
的準線與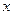 軸的交點為
軸的交點為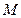 ,過點
,過點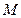 作直線
作直線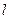 交拋物線于
交拋物線于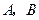 兩點.若直線
兩點.若直線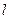 的斜率依次取
的斜率依次取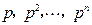 時,線段
時,線段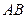 的垂直平分線與對稱軸的交點依次為
的垂直平分線與對稱軸的交點依次為 ,當
,當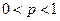 時,求
時,求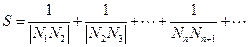 的值.
的值. 所得的弦長為
所得的弦長為 。
。