
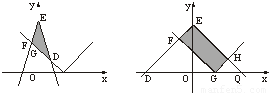 (1)證明:顯然(0,a)∈A.
(1)證明:顯然(0,a)∈A.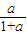 ,
,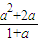 )、D(
)、D(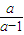 ,
,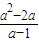 )、G(0,a).
)、G(0,a). a•
a•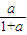 +
+ a•
a•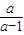 =
=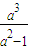 .
.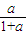 ,
,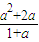 )、G(a,0)、H(
)、G(a,0)、H(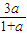 ,
,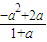 )、D(-2,0)、Q(2,0),
)、D(-2,0)、Q(2,0), ×4×2a-
×4×2a- (a+2)•
(a+2)•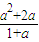 -
- (2-a)•
(2-a)•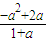 =
=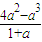 .
.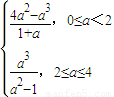
 ,∴S′=
,∴S′=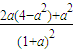 >0
>0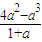 在[0,2)上是增函數(shù).∴0≤S<
在[0,2)上是增函數(shù).∴0≤S< .
.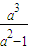 ,∴S′=
,∴S′=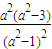 >0,
>0,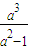 在[2,4]上是增函數(shù),∴
在[2,4]上是增函數(shù),∴ ≤S≤
≤S≤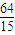 .
.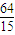 .
.

 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com