
如圖,游客在景點(diǎn)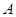 處下山至
處下山至 處有兩條路徑.一條是從
處有兩條路徑.一條是從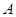 沿直道步行到
沿直道步行到 ,另一條是先從
,另一條是先從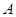 沿索道乘纜車到
沿索道乘纜車到 ,然后從
,然后從 沿直道步行到
沿直道步行到 .現(xiàn)有甲、乙兩位游客從
.現(xiàn)有甲、乙兩位游客從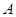 處下山,甲沿
處下山,甲沿 勻速步行,速度為
勻速步行,速度為 .在甲出發(fā)
.在甲出發(fā) 后,乙從
后,乙從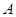 乘纜車到
乘纜車到 ,在
,在 處停留
處停留 后,再從
后,再從 勻速步行到
勻速步行到 .假設(shè)纜車勻速直線運(yùn)動(dòng)的速度為
.假設(shè)纜車勻速直線運(yùn)動(dòng)的速度為 ,索道
,索道 長為
長為 ,經(jīng)測(cè)量
,經(jīng)測(cè)量 ,
, .
.
(1)求山路 的長;
的長;
(2)假設(shè)乙先到,為使乙在 處等待甲的時(shí)間不超過
處等待甲的時(shí)間不超過 分鐘,乙步行的速度應(yīng)控制在什么范圍內(nèi)?
分鐘,乙步行的速度應(yīng)控制在什么范圍內(nèi)?
(1) 米;(2)乙步行的速度應(yīng)控制在
米;(2)乙步行的速度應(yīng)控制在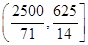
 內(nèi).
內(nèi).
解析試題分析:(1)利用同角三角函數(shù)的基本關(guān)系先求出 和
和 ,再利用內(nèi)角和定理以及誘導(dǎo)公式、兩角和的正弦公式求出
,再利用內(nèi)角和定理以及誘導(dǎo)公式、兩角和的正弦公式求出 的值,最終利用正弦定理求出
的值,最終利用正弦定理求出 的長度;(2)利用正弦定理先求出
的長度;(2)利用正弦定理先求出 的長度,然后計(jì)算甲步行至
的長度,然后計(jì)算甲步行至 處所需的時(shí)間以及乙從
處所需的時(shí)間以及乙從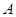 乘纜車到
乘纜車到 所需的時(shí)間,并設(shè)乙步行的速度為
所需的時(shí)間,并設(shè)乙步行的速度為 ,根據(jù)題中條件列有關(guān)
,根據(jù)題中條件列有關(guān) 的不等式,求出
的不等式,求出 即可.
即可.
試題解析:(1)∵ ,
, ,
,
∴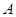 、
、 ,∴
,∴ ,
, ,
,
∴ ,
,
根據(jù) 得
得 ,
,
所以山路 的長為
的長為 米;
米;
(2)由正弦定理 得
得 (
( ),
),
甲共用時(shí)間: ,乙索道所用時(shí)間:
,乙索道所用時(shí)間: ,
,
設(shè)乙的步行速度為 ,由題意得
,由題意得 ,
,
整理得 ,
, ,
,
∴為使乙在 處等待甲的時(shí)間不超過
處等待甲的時(shí)間不超過 分鐘,乙步行的速度應(yīng)控制在
分鐘,乙步行的速度應(yīng)控制在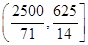
 內(nèi).
內(nèi).
考點(diǎn):1.同角三角函數(shù)的基本關(guān)系;2.內(nèi)角和定理;3.兩角和的正弦公式;4.正弦定理



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知向量
 ,設(shè)函數(shù)
,設(shè)函數(shù)
 的圖象關(guān)于直線
的圖象關(guān)于直線 對(duì)稱,其中常數(shù)
對(duì)稱,其中常數(shù)
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)將函數(shù) 的圖像向左平移
的圖像向左平移 個(gè)單位,得到函數(shù)
個(gè)單位,得到函數(shù) 的圖像,用五點(diǎn)法作出函數(shù)
的圖像,用五點(diǎn)法作出函數(shù) 在區(qū)間
在區(qū)間 的圖像.
的圖像.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)
(1)求 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)在 中,內(nèi)角A,B,C的對(duì)邊分別為
中,內(nèi)角A,B,C的對(duì)邊分別為 ,已知
,已知 ,
, 成等差數(shù)列,且
成等差數(shù)列,且 ,求邊
,求邊 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)
(1)當(dāng) 時(shí),求
時(shí),求 的最大值及相應(yīng)的x值;
的最大值及相應(yīng)的x值;
(2)利用函數(shù)y=sin 的圖象經(jīng)過怎樣的變換得到f(x)的圖象.
的圖象經(jīng)過怎樣的變換得到f(x)的圖象.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) ,
, .
.
(Ⅰ)求函數(shù) 的最小值和最小正周期;
的最小值和最小正周期;
(Ⅱ)設(shè) 的內(nèi)角
的內(nèi)角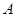 、
、 、
、 的對(duì)邊分別為
的對(duì)邊分別為 、
、 、
、 ,滿足
,滿足 ,
, 且
且 ,求
,求 、
、 的值.
的值.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com