Question

已知一幾何體的三視圖如圖(甲)示，(三視圖中已經給出各投影面頂點的標記)

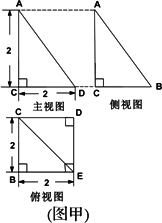
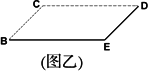
(1)在已給出的一個面上(圖乙)，畫出該幾何體的直觀圖；

(2)設點F、H、G分別為AC、AD、DE的中點，求證：FG∥平面ABE；

(3)求該幾何體的體積．

Answer 1

答案：
解析：

解：(1)該幾何體的直觀圖如圖示：　　4分 　　(說明：畫出AC平面ABCD得2分，其余2分，其他畫法可按實際酌情給分) 　　(2)證法一：取BA的中點I，連接FI、IE， 　　∵F、I分別為AC、AB的中點，∴FIBC　　5分 　　∵BC∥ED　∴FIED， 　　又EG＝ED，∴FIEG 　　∴四邊形EGFI為平行四邊形　　7分 　　∴EI∥FG 　　又∵面，面　∴FG∥平面ABE　　9分 　　證法二：由圖(甲)知四邊形CBED為正方形 　　∵F、H、G分別為AC，AD，DE的中點 　　∴FH∥CD，HG∥AE　　5分 　　∵CD∥BE，∴FH∥BE 　　∵面，面 　　∴面　　7分 　　同理可得面 　　又∵　∴平面FHG∥平面ABE　　8分 　　又∵面　∴FG∥平面ABE　　9分 　　(3)由圖甲知ACCD，ACBC， 　　∴AC平面ABCD，即AC為四棱棱錐的高　　10分 　　∵底面ABCD是一個正方形，　　12分 　　∴該幾何體的體積： 　　　　14分