函數(shù)數(shù)列
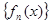
滿足:
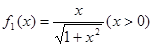
,
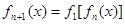
(1)求
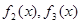
;
(2)猜想
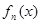
的表達(dá)式,并證明你的結(jié)論.
(1)
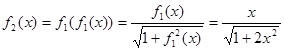
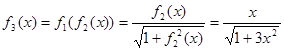
(2)猜想:
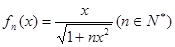
下面用數(shù)學(xué)歸納法證明:
①當(dāng)n=1時,
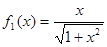
,已知,顯然成立
②假設(shè)當(dāng)
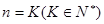
時,猜想成立,即
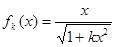
則當(dāng)
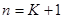
時,
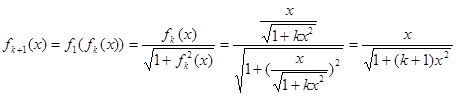
即對
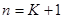
時,猜想也成立.
由①②可得
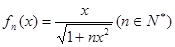
成立
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本題滿分12分)數(shù)列
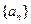
滿足
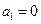
,
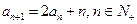
.
(1)設(shè)
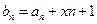
,是否存在實數(shù)
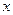
,使得
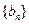
是等比數(shù)列;
(2)是否存在不小于2的正整數(shù)
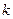
,使得
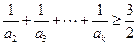
成立?若存在,求出
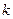
的最小值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分12分)
已知{
an}是公差不為零的等差數(shù)列,
a1=1,且
a1,
a3,
a9成等比數(shù)列.
(Ⅰ)求數(shù)列{
an}的通項; (Ⅱ)求數(shù)列
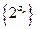
的前
n項和
Sn.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知
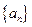
為等差數(shù)列,公差
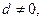
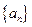
的部分項
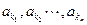
恰為等比數(shù)列,若
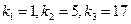
,則
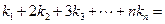
__
▲ __.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知等差數(shù)列:
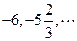
.的前
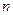
項和為
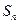
,使
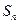
最小的
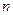
=
★ .
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
等差數(shù)列的前n項和為Sn,若S2=2,S4=10,則S6= .
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
已知數(shù)列
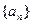
滿足
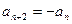
,且
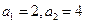
,則該數(shù)列的前509項的和為
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
數(shù)列
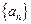
中,
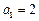
,
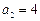
,對于函數(shù)
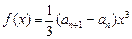
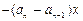
(其中
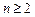
,
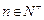
),有
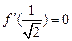
,則數(shù)列
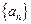
的通項公式為__________
查看答案和解析>>

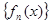 滿足:
滿足: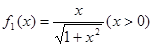 ,
,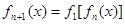
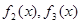 ;
;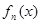 的表達(dá)式,并證明你的結(jié)論.
的表達(dá)式,并證明你的結(jié)論. 閱讀快車系列答案
閱讀快車系列答案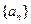 滿足
滿足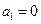 ,
,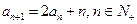 .
.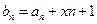 ,是否存在實數(shù)
,是否存在實數(shù)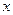 ,使得
,使得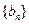 是等比數(shù)列;
是等比數(shù)列;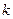 ,使得
,使得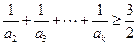 成立?若存在,求出
成立?若存在,求出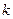 的最小值;若不存在,說明理由.
的最小值;若不存在,說明理由. 的前n項和Sn.
的前n項和Sn.