
分析 設出$\overrightarrow{a}$、$\overrightarrow{b}$的坐標,利用$\overrightarrow{a}$+$\overrightarrow{b}$與$\overrightarrow{a}$-$\overrightarrow{b}$列出方程,求出$\overrightarrow{a}$、$\overrightarrow{b}$的坐標,再求$\overrightarrow{a}$,$\overrightarrow{b}$夾角的余弦值.
解答 解:設$\overrightarrow{a}$=(x1,y1),$\overrightarrow{b}$=(x2,y2),
∵$\overrightarrow{a}$+$\overrightarrow{b}$=(5,-10),$\overrightarrow{a}$-$\overrightarrow{b}$=(3,6),
∴$\left\{\begin{array}{l}{{x}_{1}{+x}_{2}=5}\\{{x}_{1}{-x}_{2}=3}\end{array}\right.$,且$\left\{\begin{array}{l}{{y}_{1}{+y}_{2}=-10}\\{{y}_{1}{-y}_{2}=6}\end{array}\right.$,
解得x1=4,x2=1,y1=-2,y1=-8,
∴$\overrightarrow{a}$=(4,-2),$\overrightarrow{b}$=(1,-8);
∴$\overrightarrow{a}$,$\overrightarrow{b}$夾角的余弦值為:
cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{4×1+(-2)×(-8)}{\sqrt{{4}^{2}{+(-2)}^{2}}×\sqrt{{1}^{2}{+(-8)}^{2}}}$=$\frac{2\sqrt{13}}{13}$.
故答案為:$\frac{{2\sqrt{13}}}{13}$.
點評 本題考查了平面向量的坐標表示以及求向量夾角的應用問題,是基礎題目


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
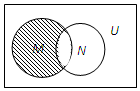
| A. | {-2,-1} | B. | {0,1,2} | C. | {-2,-1,3} | D. | {-2,-1,0} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com