分析:(1)以D為坐標原點,DA、DB、DD
1分別為x、y、z軸建立空間直角坐標系(D
1是C
1B
1的中點),建立空間直角坐標系,用坐標表示點與向量,證明
•=0且
•=0,即可證得B
1F⊥平面ADF;
(2)求得平面AA
1B
1B的一個法向量
=(a,2a,0),利用cos<
,
>=
,即可求得二面角的余弦值.
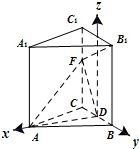
解答:(1)證明:以D為坐標原點,DA、DB、DD
1分別為x、y、z軸建立空間直角坐標系(D
1是C
1B
1的中點),
則A(2
a,0,0),B(0,a,0),F(0,-a,2a),B
1(0,a,3a),(4分)
=(0,-2a,-a),
=(0,-a,2a),
=(2a,0,0),
由
•=0且
•=0,得B
1F⊥DF,B
1F⊥DA,
∵DF∩DA=D,且DF、DA?平面ADF
∴B
1F⊥平面ADF;(6分)
(2)由(1)知
=(2a,-a,0),
=(0,0,3a),
設平面AA
1B
1B的一個法向量為
=(x,y,0),
則
•=0且
•=0,可取
=(a,2a,0),(8分)
由cos<
,
>=
=-
即所求二面角的余弦值是
.(13分)
點評:本題考查線面垂直,考查面面角,解題的關鍵是建立空間直角坐標系,利用向量方法解決立體幾何問題,屬于中檔題.

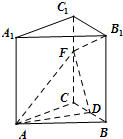 直三棱柱ABC-A1B1C1中AB=AC=AA1=3a,BC=2a,D是BC的中點,F是C1C上一點,且CF=2a.
直三棱柱ABC-A1B1C1中AB=AC=AA1=3a,BC=2a,D是BC的中點,F是C1C上一點,且CF=2a.


 閱讀快車系列答案
閱讀快車系列答案 如圖,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直線B1C與平面ABC成30°角.
如圖,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=BB1=a,直線B1C與平面ABC成30°角. 如圖,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,則BC1與平面AB B1 A1所成角的正弦值是
如圖,在直三棱柱ABC-A1 B1 C1中,AA1=1,AC⊥BC,AC=BC=2,則BC1與平面AB B1 A1所成角的正弦值是







