tan18°+tan27°+tan18°•tan27°=________.
1
分析:觀察發現:18°+27°=45°,故利用兩角和的正切函數公式表示出tan(18°+27°),利用特殊角的三角函數值化簡,變形后即可得到所求式子的值.
解答:由tan45°=tan(18°+27°)=
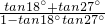
=1,
得到tan18°+tan27°=1-tan18°tan27°,
則tan18°+tan27°+tan18°•tan27°=1.
故答案為:1
點評:此題考查了兩角和與差得正切函數公式,以及特殊角的三角函數值.觀察所求式子中的角度的和為45°,聯想到利用45°角的正切函數公式是解本題的關鍵.
