
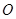 為圓心、
為圓心、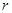 公里為半徑的圓形保護(hù)區(qū),從保護(hù)區(qū)邊緣起,在城中心
公里為半徑的圓形保護(hù)區(qū),從保護(hù)區(qū)邊緣起,在城中心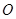 正東方向上有一條高速公路
正東方向上有一條高速公路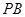 、西南方向上有一條一級公路
、西南方向上有一條一級公路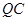 ,現(xiàn)要在保護(hù)區(qū)邊緣PQ弧上選擇一點A作為出口,建一條連接兩條公路且與圓
,現(xiàn)要在保護(hù)區(qū)邊緣PQ弧上選擇一點A作為出口,建一條連接兩條公路且與圓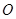 相切的直道
相切的直道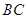 .已知通往一級公路的道路
.已知通往一級公路的道路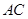 每公里造價為
每公里造價為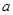 萬元,通往高速公路的道路
萬元,通往高速公路的道路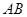 每公里造價是
每公里造價是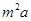 萬元,其中
萬元,其中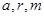 為常數(shù),設(shè)
為常數(shù),設(shè)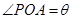 ,總造價為
,總造價為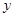 萬元.
萬元.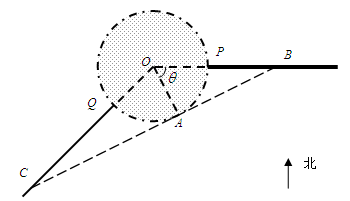
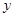 表示成
表示成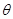 的函數(shù)
的函數(shù)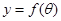 ,并求出定義域;
,并求出定義域;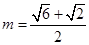 時,如何確定A點的位置才能使得總造價最低?
時,如何確定A點的位置才能使得總造價最低?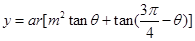 ,定義域為:
,定義域為: ,(2)當(dāng)
,(2)當(dāng)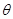 取
取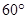 ,即A點在O東偏南
,即A點在O東偏南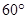 的方向上,總造價最低. 16分
的方向上,總造價最低. 16分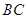 與圓O相切于A,
與圓O相切于A,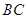 ,在
,在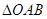 中,
中,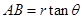 , 2分
, 2分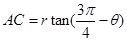 4分
4分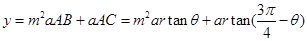 ,
,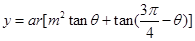 , 6分
, 6分 8分
8分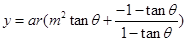
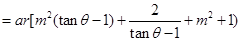 11分
11分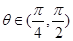 ,∴
,∴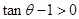 ,
,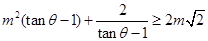 13分
13分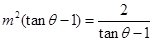 時取等號,即
時取等號,即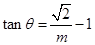 ,
,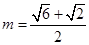 ,∴
,∴ ,∴
,∴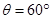 15分
15分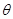 取
取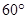 ,即A點在O東偏南
,即A點在O東偏南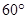 的方向上,總造價最低. 16分
的方向上,總造價最低. 16分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
A.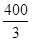 米 米 | B. 米 米 | C.200 米 米 | D.200米 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com