
平面內(nèi)動(dòng)點(diǎn) 到點(diǎn)
到點(diǎn)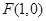 的距離等于它到直線
的距離等于它到直線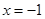 的距離,記點(diǎn)
的距離,記點(diǎn) 的軌跡為曲
的軌跡為曲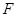 .
.
(Ⅰ)求曲線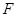 的方程;
的方程;
(Ⅱ)若點(diǎn)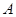 ,
,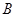 ,
, 是
是 上的不同三點(diǎn),且滿足
上的不同三點(diǎn),且滿足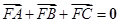 .證明:
.證明: 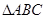 不可能為直角三角形.
不可能為直角三角形.
(1)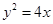
(2)利用向量的關(guān)系式來得到坐標(biāo)關(guān)系式,然后借助于反證法來說明不成立。
【解析】
試題分析:解法一:(Ⅰ)由條件可知,點(diǎn) 到點(diǎn)
到點(diǎn)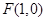 的距離與到直線
的距離與到直線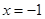 的距離相等, 所以點(diǎn)
的距離相等, 所以點(diǎn) 的軌跡是以
的軌跡是以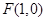 為焦點(diǎn),
為焦點(diǎn),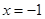 為準(zhǔn)線的拋物線,其方程為
為準(zhǔn)線的拋物線,其方程為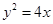 . 4分
. 4分
(Ⅱ)假設(shè)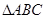 是直角三角形,不失一般性,設(shè)
是直角三角形,不失一般性,設(shè) ,
,
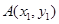 ,
,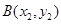 ,
,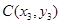 ,則由
,則由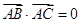 ,
,
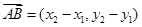 ,
,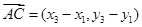 ,
,
所以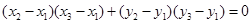 .
6分
.
6分
因?yàn)?img
src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013081312565744718282/SYS201308131258127335558406_DA.files/image014.png">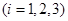 ,
,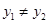 ,
,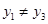 ,
,
所以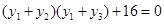 .
8分
.
8分
又因?yàn)?img
src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013081312565744718282/SYS201308131258127335558406_DA.files/image019.png">,所以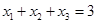 ,
,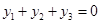 ,
,
所以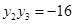 . ①
. ①
又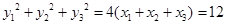 ,
,
所以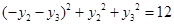 ,即
,即 . ② 10分
. ② 10分
由①,②得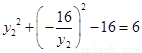 ,所以
,所以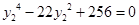 . ③
. ③
因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013081312565744718282/SYS201308131258127335558406_DA.files/image028.png">.
所以方程③無解,從而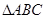 不可能是直角三角形.
12分
不可能是直角三角形.
12分
解法二:(Ⅰ)同解法一
(Ⅱ)設(shè)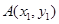 ,
,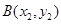 ,
,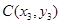 ,由
,由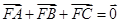 ,
,
得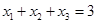 ,
,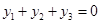 .
6分
.
6分
由條件的對稱性,欲證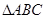 不是直角三角形,只需證明
不是直角三角形,只需證明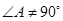 .
.
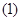 當(dāng)
當(dāng)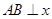 軸時(shí),
軸時(shí),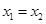 ,
,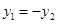 ,從而
,從而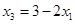 ,
,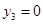 ,
,
即點(diǎn)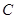 的坐標(biāo)為
的坐標(biāo)為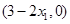 .
.
由于點(diǎn)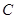 在
在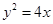 上,所以
上,所以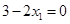 ,即
,即 ,
,
此時(shí)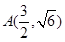 ,
,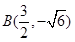 ,
,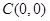 ,則
,則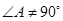 . 8分
. 8分
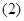 當(dāng)
當(dāng)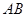 與
與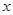 軸不垂直時(shí),
軸不垂直時(shí),
設(shè)直線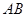 的方程為:
的方程為: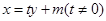 ,代入
,代入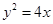 ,
,
整理得: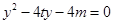 ,則
,則 .
.
若 ,則直線
,則直線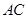 的斜率為
的斜率為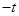 ,同理可得:
,同理可得: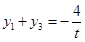 .
.
由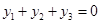 ,得
,得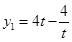 ,
,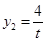 ,
,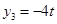 .
.
由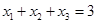 ,可得
,可得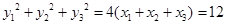 .
.
從而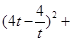
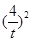
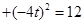 ,
,
整理得: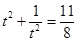 ,即
,即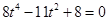 ,①
,①
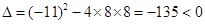 .
.
所以方程①無解,從而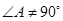 .
11分
.
11分
綜合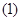 ,
,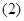 ,
, 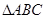 不可能是直角三角形.
12分
不可能是直角三角形.
12分
考點(diǎn):拋物線的標(biāo)準(zhǔn)方程、直線與圓錐曲線的位置關(guān)系
點(diǎn)評:本小題考查拋物線的標(biāo)準(zhǔn)方程、直線與圓錐曲線的位置關(guān)系等基礎(chǔ)知識(shí),考查推理論證能力、運(yùn)算求解能力,考查化歸與轉(zhuǎn)化思想、分類與整合思想、數(shù)形結(jié)合思想等


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
(本小題滿分13分)
已知平面內(nèi)一動(dòng)點(diǎn)![]() 到點(diǎn)
到點(diǎn)![]() 的距離與點(diǎn)
的距離與點(diǎn)![]() 到
到![]() 軸的距離的差等于1.
軸的距離的差等于1.
(Ⅰ)求動(dòng)點(diǎn)![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過點(diǎn)![]() 作兩條斜率存在且互相垂直的直線
作兩條斜率存在且互相垂直的直線![]() ,設(shè)
,設(shè)![]() 與軌跡
與軌跡![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,
,![]() 與軌跡
與軌跡![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年江西省高三4月月考數(shù)學(xué)文理合卷試卷(解析版) 題型:解答題
已知平面內(nèi)一動(dòng)點(diǎn)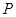 到點(diǎn)
到點(diǎn)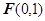 的距離與點(diǎn)
的距離與點(diǎn)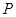 到
到 軸的距離的差等于1.(I)求動(dòng)點(diǎn)
軸的距離的差等于1.(I)求動(dòng)點(diǎn)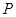 的軌跡
的軌跡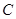 的方程;(II)過點(diǎn)
的方程;(II)過點(diǎn)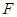 作兩條斜率存在且互相垂直的直線
作兩條斜率存在且互相垂直的直線 ,設(shè)
,設(shè)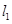 與軌跡
與軌跡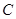 相交于點(diǎn)
相交于點(diǎn)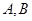 ,
, 與軌跡
與軌跡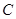 相交于點(diǎn)
相交于點(diǎn)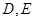 ,求
,求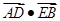 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012-2013學(xué)年江西南昌10所省高三第二次模擬數(shù)學(xué)試卷(五)(解析版) 題型:解答題
已知平面內(nèi)一動(dòng)點(diǎn)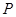 到點(diǎn)
到點(diǎn)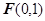 的距離與點(diǎn)
的距離與點(diǎn)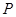 到
到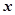 軸的距離的差等于1.(I)求動(dòng)點(diǎn)
軸的距離的差等于1.(I)求動(dòng)點(diǎn)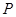 的軌跡
的軌跡 的方程;(II)過點(diǎn)
的方程;(II)過點(diǎn)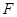 作兩條斜率存在且互相垂直的直線
作兩條斜率存在且互相垂直的直線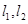 ,設(shè)
,設(shè) 與軌跡
與軌跡 相交于點(diǎn)
相交于點(diǎn)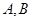 ,
,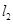 與軌跡
與軌跡 相交于點(diǎn)
相交于點(diǎn) ,求
,求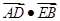 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:湖南省十二校2011-2012學(xué)年高三第一次聯(lián)考試題-數(shù)學(xué)(文) 題型:解答題
已知平面內(nèi)一動(dòng)點(diǎn)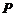 到點(diǎn)
到點(diǎn)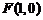 的距離等于它到直線
的距離等于它到直線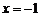 的距離.
的距離.
(Ⅰ)求動(dòng)點(diǎn)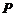 的軌跡
的軌跡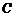 的方程;
的方程;
(Ⅱ)若直線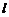 與曲線
與曲線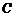 交于
交于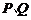 兩點(diǎn),且
兩點(diǎn),且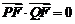 ,又點(diǎn)
,又點(diǎn)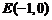 ,求
,求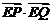 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com