
設
0<x<1,a>0,且a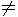 1,比較
1,比較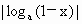 與
與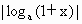 的大小.
的大小. |
解法一:當 a>1時,∵0<x<1則1+x>1,0<1-x<1,∴ 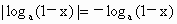 , ,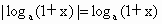 ,則有 ,則有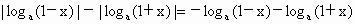 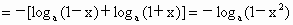 . .
∵ a>1,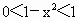 ∴ ∴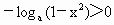 .∴ .∴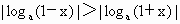 . .
當 0<a<1時,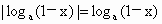 . .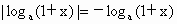 , ,
則有  . .
∵ 0<a<1,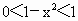 ,∴ ,∴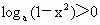 .∴ .∴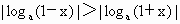 . .
因此,當 0<x<1,a>0,且a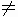 1時,總有 1時,總有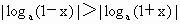 . .
解法二: 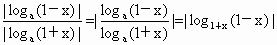 . .
∵ 1+x>1,0<1-x<1,∴ 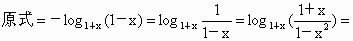
∵ 1+x>1,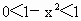 , ,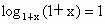 , ,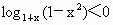 , ,
∴  . .
即 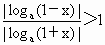 ,∴ ,∴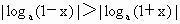 . .
(1) 此題的解答過程中有兩個關鍵的步驟:一是比較兩個實數大小的出發點和基本方法(作差比較法與作商比較法).二是利用對數函數的性質處理兩個絕對值符號和進行對數式的變換與計算.(2) 比較以上解法各有優點,解法1中,分0<a<1和a>1兩種情況進行討論的思想方法是具有普通意義的;而解法2比解法1簡便,其原因是充分注意到了所需要比較大小的是兩個正數,同時巧妙地運用了換底公式,從而避開了對底數a的討論.(3) 含絕對值的問題,一般要去掉絕對值研究,這是一個基本觀點.去絕對值時,注意對誰取絕對值就對誰討論.|f(x)|當f(x)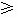 0時為f(x),當f(x)<0時為-f(x). 0時為f(x),當f(x)<0時為-f(x). |


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n |
| 1+x2 |
查看答案和解析>>
科目:高中數學 來源:2012年人教B版高中數學必修一3.2對數函數練習卷(二)(解析版) 題型:解答題
設0<x<1,a>0且a≠1,試比較|loga(1-x)|與|loga(1+x)|的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com