已知函數f(x)=3x,且f-1(18)=a+2,g(x)=3ax-4x的定義域為[0,1].
(1)求g(x)的解析式;
(2)求g(x)的單調區間,確定其單調性并用定義證明;
(3)求g(x)的值域.
【答案】
分析:(1)先由函數f(x)=3
x且f
-1(18)=a+2解出3
a的值,整體代入g(x)=3
ax-4x中得到g(x)=2
x-4x,
(2)對g(x)=2
x-4x求導,用導數判斷函數在[-1,1]上的單調性;
(3)由(2)的結論根據其單調性求值域.
解答:解:(1)∵f(x)=3
x且f(a+2)=3
a+2=18,
∴3
a=2.
∴g(x)=3
ax-4
x=(3
a)
x-4
x,
∴g(x)=2
x-4
x.
(2)∵函數g(x)的定義域為[0,1],令t=2
x,
∵x∈[0,1],函數t在區間[0,1]上單調遞增,
且t∈[1,2],則g(x)=t-t
2在[1,2]上單調遞減,
∴g(x)在[0,1]上單調遞減.
證明如下:設x
1,x
2∈[0,1]且x
1<x
2,則
g(x
2)-g(x
1)
=
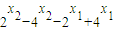
=
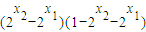
∵0≤x
1<x
2≤1,
∴
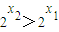
,
且

.
∴
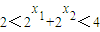
.
∴
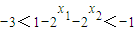
,可知
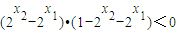
.
∴g(x
2)<g(x
1).
∴函數g(x)在[0,1]上為減函數.
(3)∵g(x)在[0,1]上為減函數,
又x∈[0,1],
故有g(1)≤g(x)≤g(0).
∵g(1)=-2,g(0)=0,
∴函數g(x)的值域為[-2,0].
點評:本題的考點是指數函數單調性的應用,考查運用指數函數的單調性求值域,合理的正確的轉化是求解成功的關鍵.

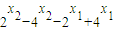 =
=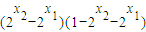
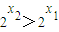 ,
, .
.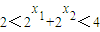 .
.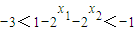 ,可知
,可知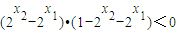 .
.

 字詞句段篇系列答案
字詞句段篇系列答案