
分析 (1)代值計算,并猜想結論,
(2)用數學歸納法證明:當n=1時,去證明等式成立;假設當n=k時,等時成立,用上歸納假設后,去證明當n=k+1時,等式也成立即可.
(3)用數學歸納法證明,當n=1時,去證明不等式成立;假設當n=k時,不等時成立,用上歸納假設后,去證明當n=k+1時,不等式也成立即可
解答 解:(1)當n=1時,${a_1}={S_1}=\frac{1}{2}a_1^2+\frac{1}{2}$,得a1=1; ${a_1}+{a_2}={S_2}=\frac{1}{2}a_2^2+1$,得a2=2${a_1}+{a_2}+{a_3}={S_3}=\frac{1}{2}a_3^2+\frac{3}{2}$,得a3=3,
猜想an=n
(2)證明:(ⅰ)當n=1時,顯然成立
(ⅱ)假設當n=k時,ak=k
則當n=k+1時,${a_{k+1}}={S_{k+1}}-{S_k}=\frac{1}{2}a_{k+1}^2+\frac{k+1}{2}-({\frac{1}{2}a_k^2+\frac{k}{2}})$
=$\frac{1}{2}a_{k+1}^2+\frac{k+1}{2}-({\frac{1}{2}{k^2}+\frac{k}{2}})$
整理得:$a_{k+1}^2-2{a_{k+1}}-{k^2}+1=0$,即[ak+1-(k+1)][ak+1+(k-1)]=0
結合an>0,解得ak+1=k+1,
于是對于一切的自然數n∈N*,都有an=n.
(3)證明:由(2)可知an=n,(ⅰ)當n=1時,不等式顯然成立,
(ⅱ)假設當n=k時,$1+\frac{1}{{\sqrt{2}}}+…+\frac{1}{{\sqrt{k}}}>2(\sqrt{k+1}-1)$
則當n=k+1時,$1+\frac{1}{{\sqrt{2}}}+\frac{1}{{\sqrt{3}}}+…+\frac{1}{{\sqrt{k}}}+\frac{1}{{\sqrt{k+1}}}>2(\sqrt{k+1}-1)+\frac{1}{{\sqrt{k+1}}}$
∵2($\sqrt{k+2}$-1)-2($\sqrt{k+1}$-1)-$\frac{1}{\sqrt{k+1}}$=2$\sqrt{k+2}$-2$\sqrt{k+1}$-$\frac{1}{\sqrt{k+1}}$=$\frac{2\sqrt{(k+1)(k+2)}-2(k+1)-1}{\sqrt{k+1}}$
=$\frac{2\sqrt{(k+1)(k+2)}-2k-3}{\sqrt{k+1}}$=$\frac{\sqrt{4{k}^{2}+12k+8}-\sqrt{4{k}^{2}+12k+9}}{\sqrt{k+1}}$<0,
∴$2(\sqrt{k+1}-1)+\frac{1}{{\sqrt{k+1}}}>2(\sqrt{k+2}-1)$,∴$1+\frac{1}{{\sqrt{2}}}+…+\frac{1}{{\sqrt{k}}}+\frac{1}{{\sqrt{k+1}}}>2(\sqrt{k+2}-1)$,
∴n=k+1時,不等式也成立,∴?n∈N*,原不等式成立
點評 本題考查數學歸納法,用好歸納假設是關鍵,考查邏輯推理與證明的能力,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
| A. | -7 | B. | -1 | C. | $\frac{13}{3}$ | D. | -1或-7 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
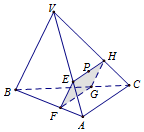 如圖所示,在四面體VABC木塊中,P為△VAC的重心,這點P作截面EFGH,若截面EFGH是平行四邊形,則該截面把木塊分成兩部分體積之比為$\frac{7}{20}$. (埴體積小與體積大之比)
如圖所示,在四面體VABC木塊中,P為△VAC的重心,這點P作截面EFGH,若截面EFGH是平行四邊形,則該截面把木塊分成兩部分體積之比為$\frac{7}{20}$. (埴體積小與體積大之比)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com